Linear Regression with Multiple Variables.

1. Multivariate Linear Regression

I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.

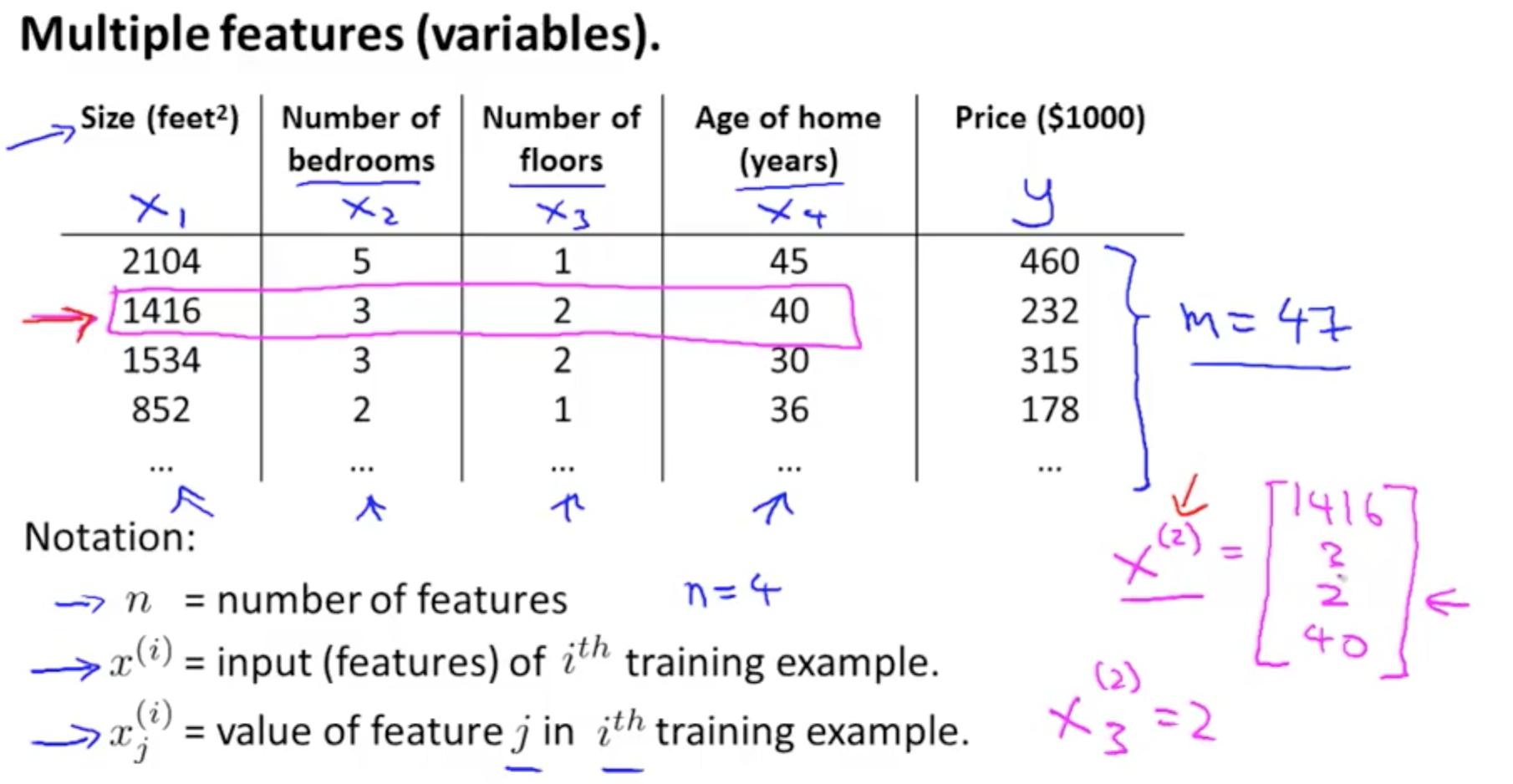
1a. Multiple Features (Variables)

  • X1, X2, X3, X4 and more alt text
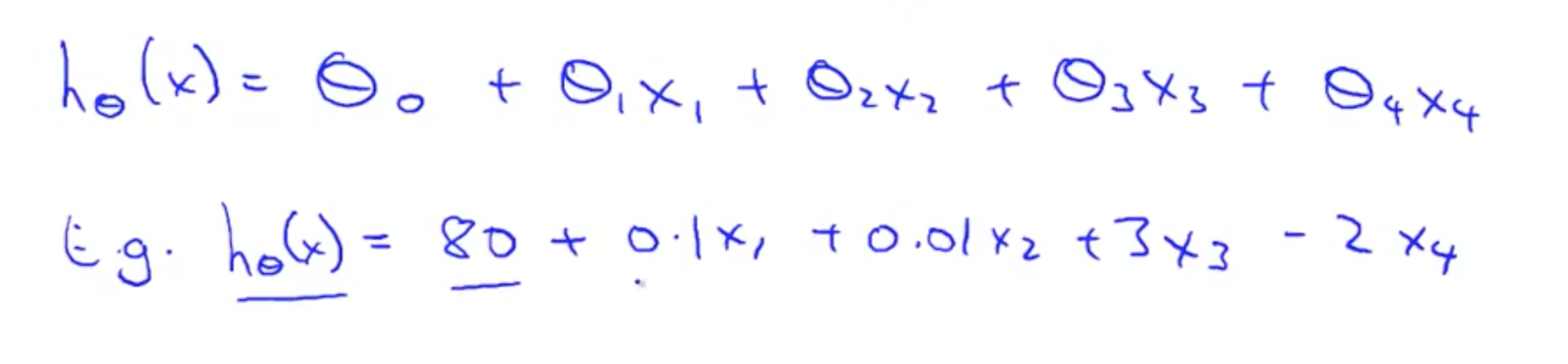
  • New hypothesis alt text
  • Multivariate linear regression
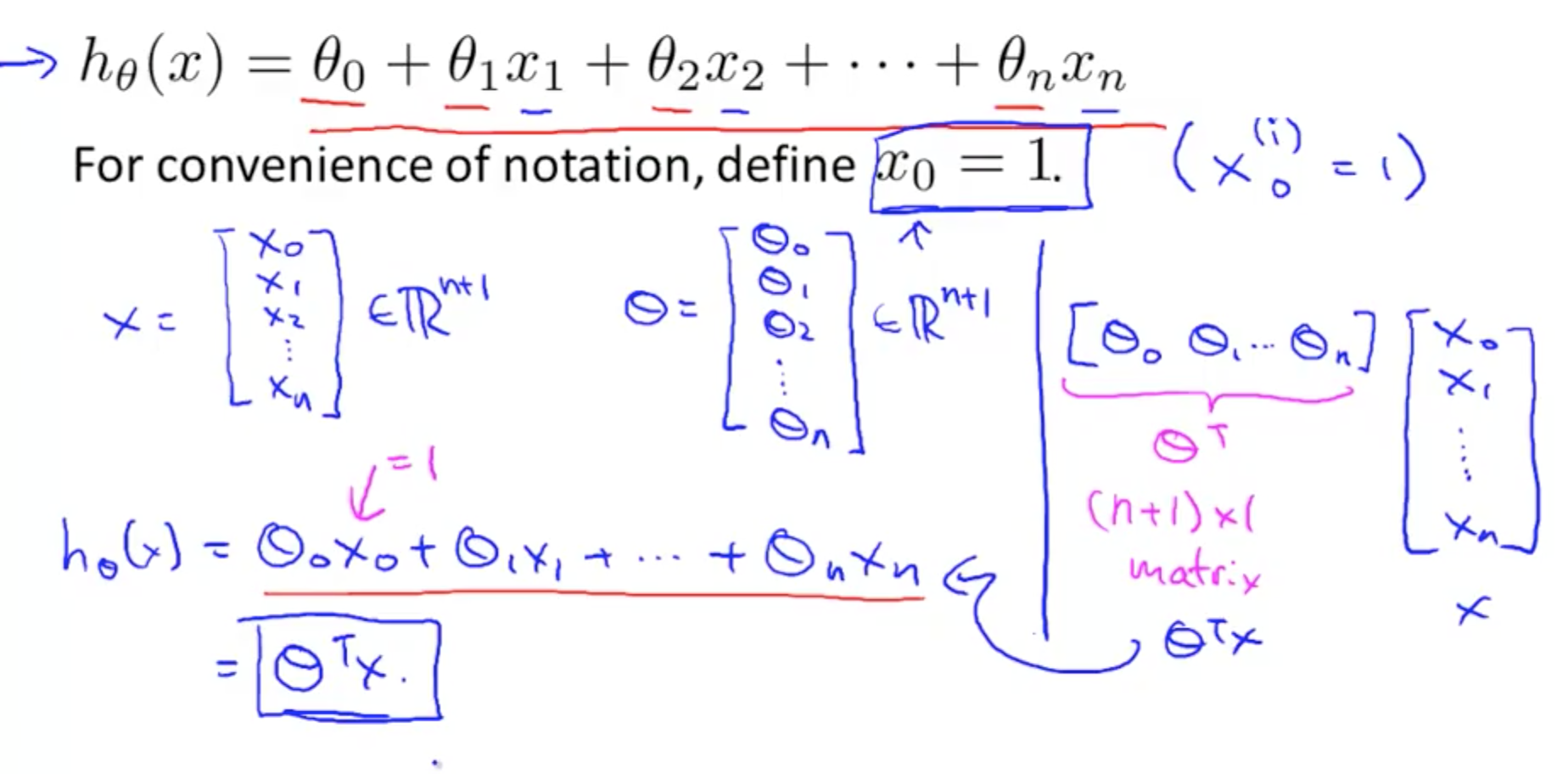
    • Can reduce hypothesis to single number with a transposed theta matrix multiplied by x matrix alt text

1b. Gradient Descent for Multiple Variables

  • Summary alt text alt text
  • New Algorithm alt text

1c. Gradient Descent: Feature Scaling

  • Ensure features are on similar scale
    • Gradient descent will take longer to reach the global minimum when the features are not on a similar scale
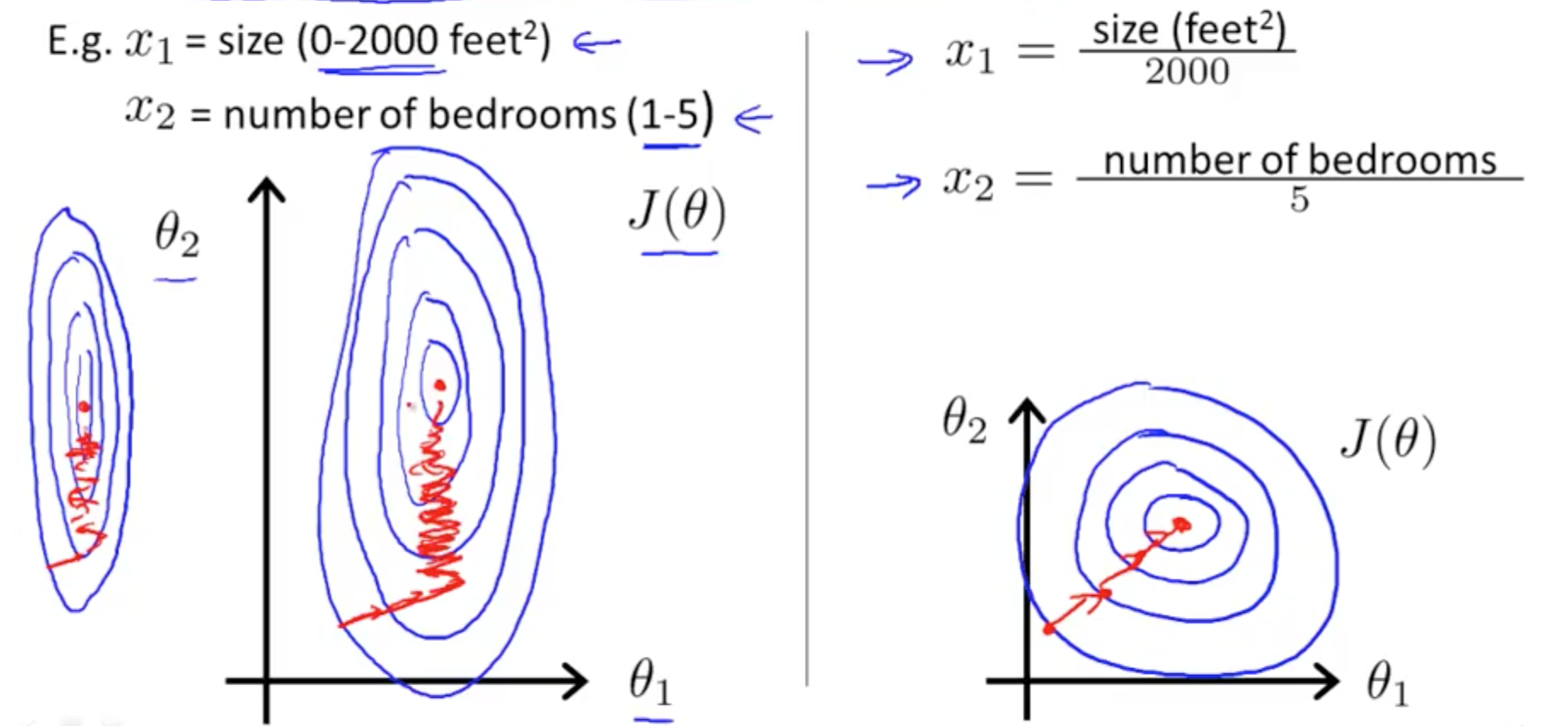
    • Feature scaling allows you to reach the global minimum faster alt text
  • So long they’re close enough, need not be between 1 and -1 alt text
  • Mean normalization alt text

1d. Gradient Descent: Checking

  • Can you a graph
    • x-axis: number of iterations
    • y-axis: min J(theta)
  • Or use automatic convergence test
    • Tough to gauge epsilon alt text
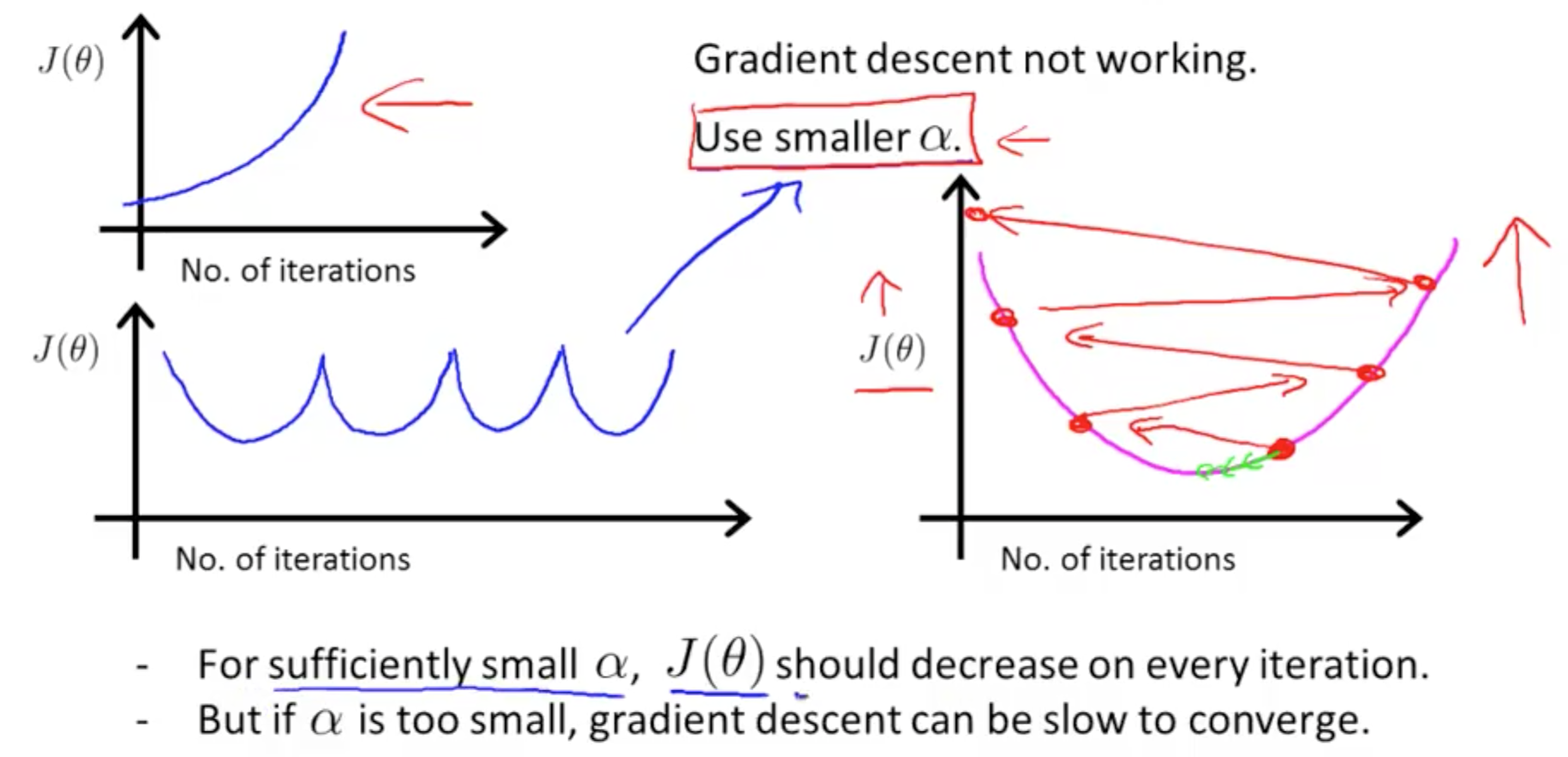
  • Gradient descent that is not working (large learning rate) alt text

1e. Gradient Descent: Learning Rate

  • Alpha (Learning Rate) too small: slow convergence
  • Alpha (Learning Rate) too large:
    • J(theta) may not decrease on every iteration
    • May not converge (diverge)
  • Start with 0.001 and increase x3 each time until you reach an acceptable alpha
    • Choose a slightly smaller number than that acceptable alpha value

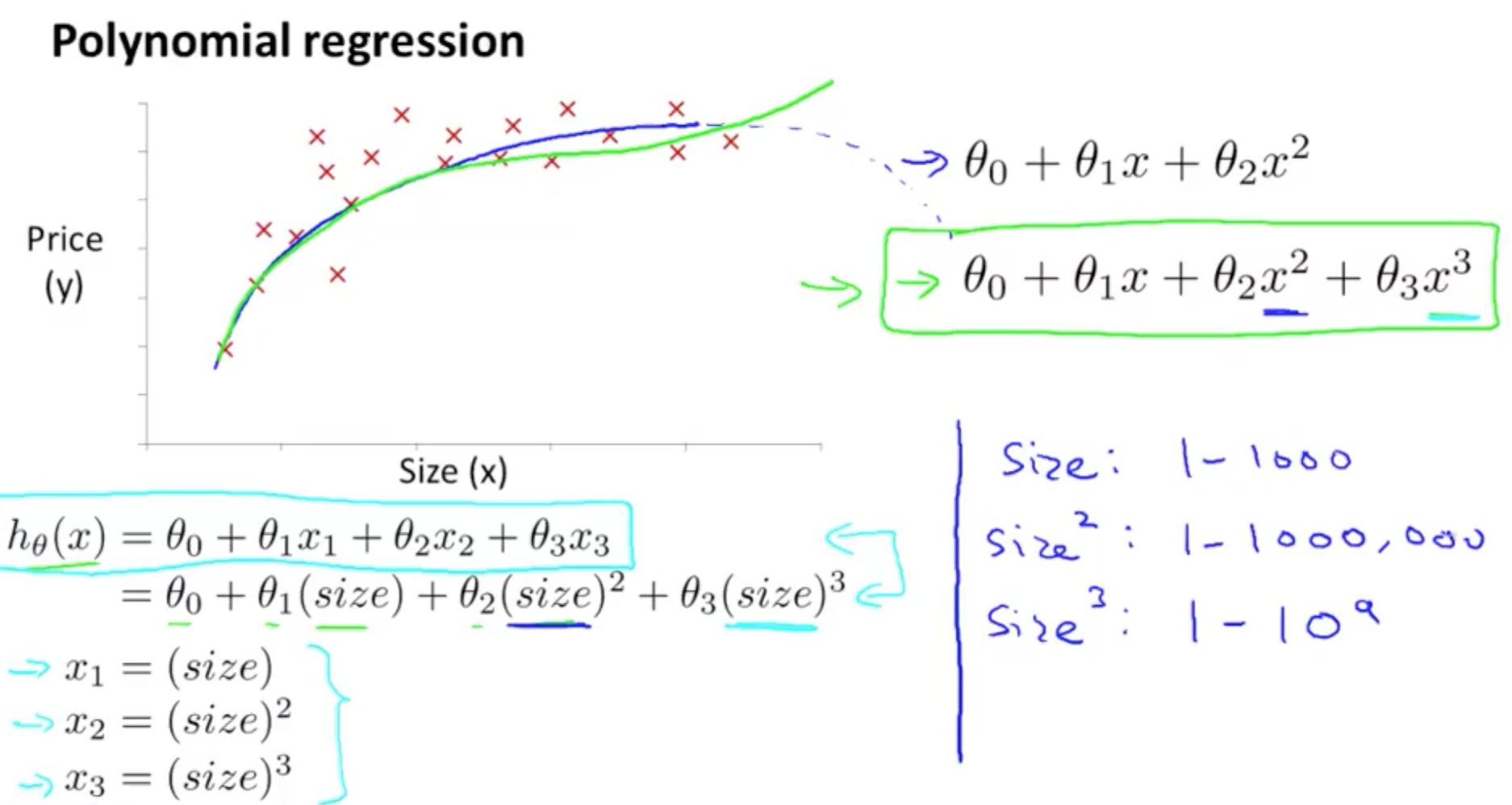
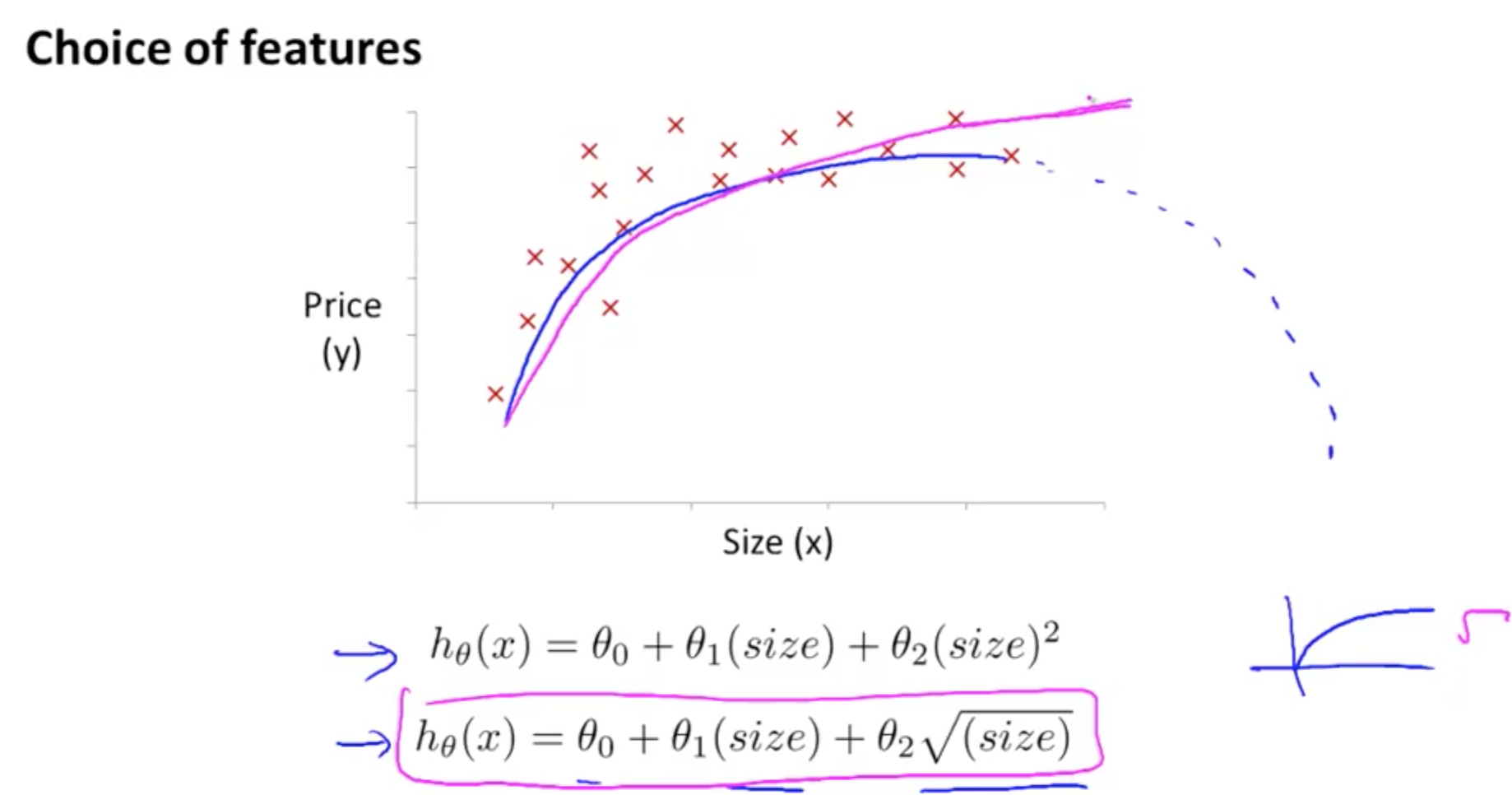
1f. Features and Polynomial Regression

  • Ensure the features capture the pattern
    • Doesn’t make sense to choose quadratic equation for house prices
    • Use cubic or square root
  • There are automatic algorithms, and this will be discussed later alt text alt text

2. Computing Parameters Analytically

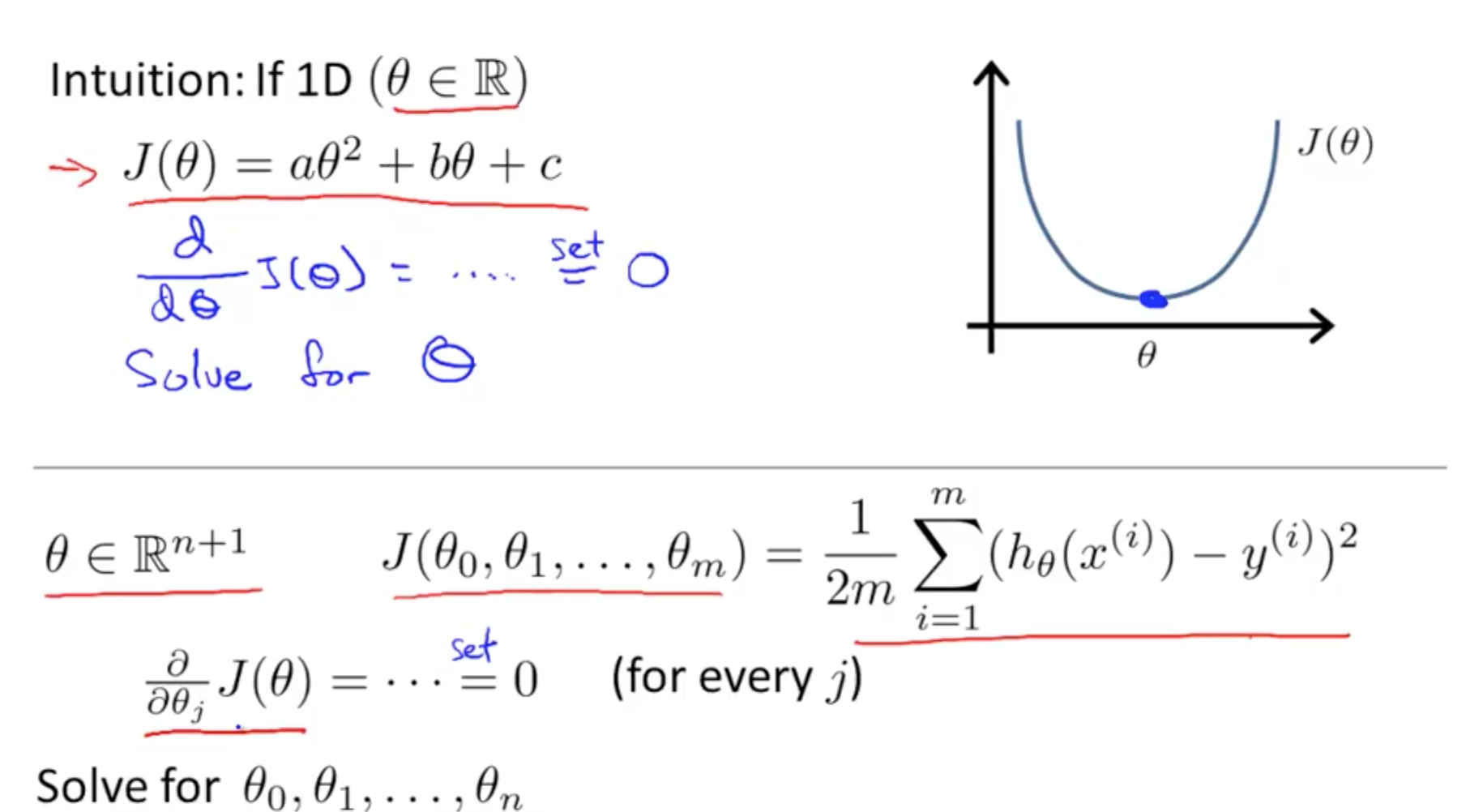
2a. Normal Equation

  • Method to solve for theta analytically
  • If theta is real number
    • Minimise J(theta) is to take the derivative and equate to zero
    • Solve for theta
  • If theta is not
    • Take partial derivative and equate to zero
    • Solve for all thetas alt text
  • Minimise Cost Function: Specific Example
    • X: m x (n + 1)
      • m: number of training examples
      • n: number of features
    • X_transpose: (n + 1) x m
    • X_transpose * X: (n + 1) x m * m x (n + 1) = (n + 1) x (n + 1)
    • (X_transpose * X)^-1 * X_transpose: (n + 1) x (n + 1) * (n + 1) x m = (n + 1) x m
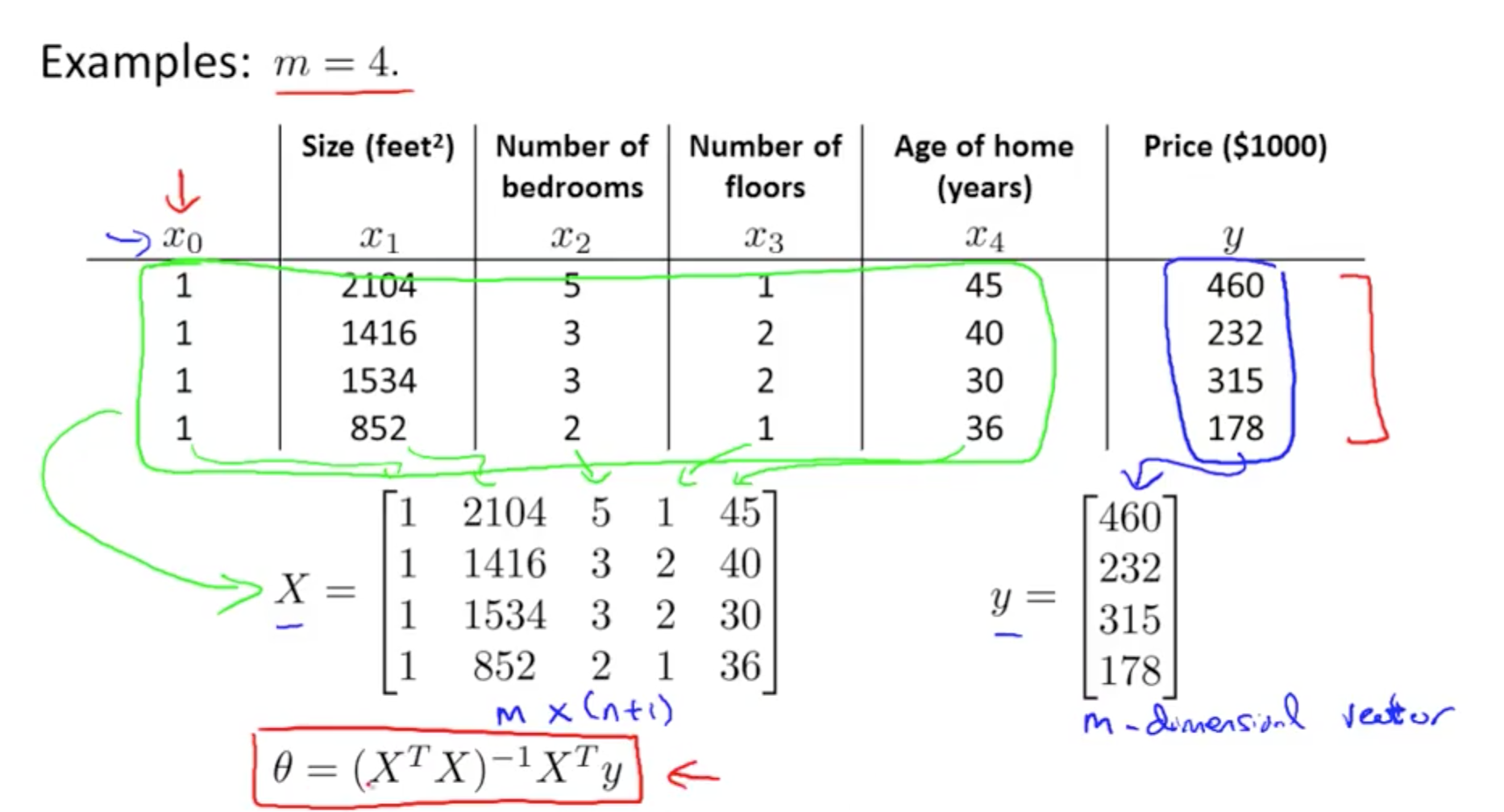
    • theta = (n + 1) x m * m x 1 = (n + 1) x 1 alt text
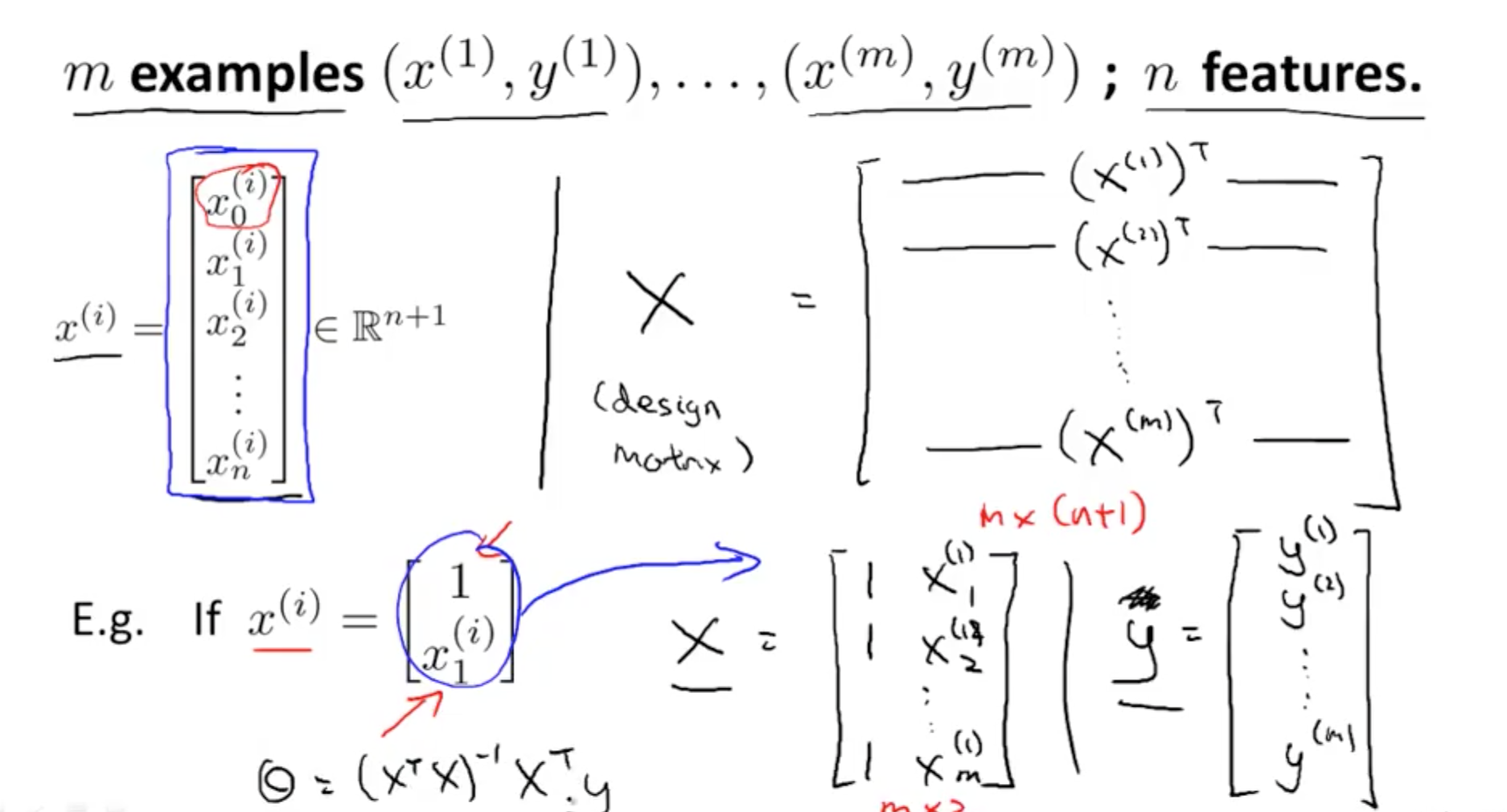
  • Minimise Cost Function: General alt text
  • Minimise Cost: Octave Code
    • No need for feature scaling using normal equation
    • pinv (X' * X) * X' * y
  • Gradient Descent vs Normal Equation
Gradient Descent Normal Equation
Need to choose alpha No need to choose alpha
Needs many iterations Don’t need to iterate
Works with large n (10,000) Slow if n is large (100, 1000 is fine)
Number of features > 1000 So long number features < 1000

2b. Normal Equation Non-invertibility

  • What happens if X_transpose * X is non-invertible (singular or degenerate)
    • pinv (X' * X) * X' * y
    • This works regardless if it is non-invertible
  • Intuition of non-invertibility
    • Causes of non-invertibility alt text
    • Delete redundant features to solve non-invertibility problem
    • Delete some features or use regularization
Tags: machine_learning