Learning Curve Theory

Graph that compares the performance of a model on training and testing data over a varying number of training instances
We should generally see performance improve as the number of training points increases
When we separate training and testing sets and graph them individually
- We can get an idea of how well the model can generalize to new data
Learning curve allows us to verify when a model has learning as much as it can about the data
When it occurs
1. The performances on the training and testing sets reach a plateau
2. There is a consistent gap between the two error rates
The key is to find the sweet spot that minimizes bias and variance by finding the right level of model complexity
Of course with more data any model can improve, and different models may be optimal
For a more in-depth theoretical coverage of learning curves, you can view a guide by Andrew Ng that I have compiled here

Types of learning curves

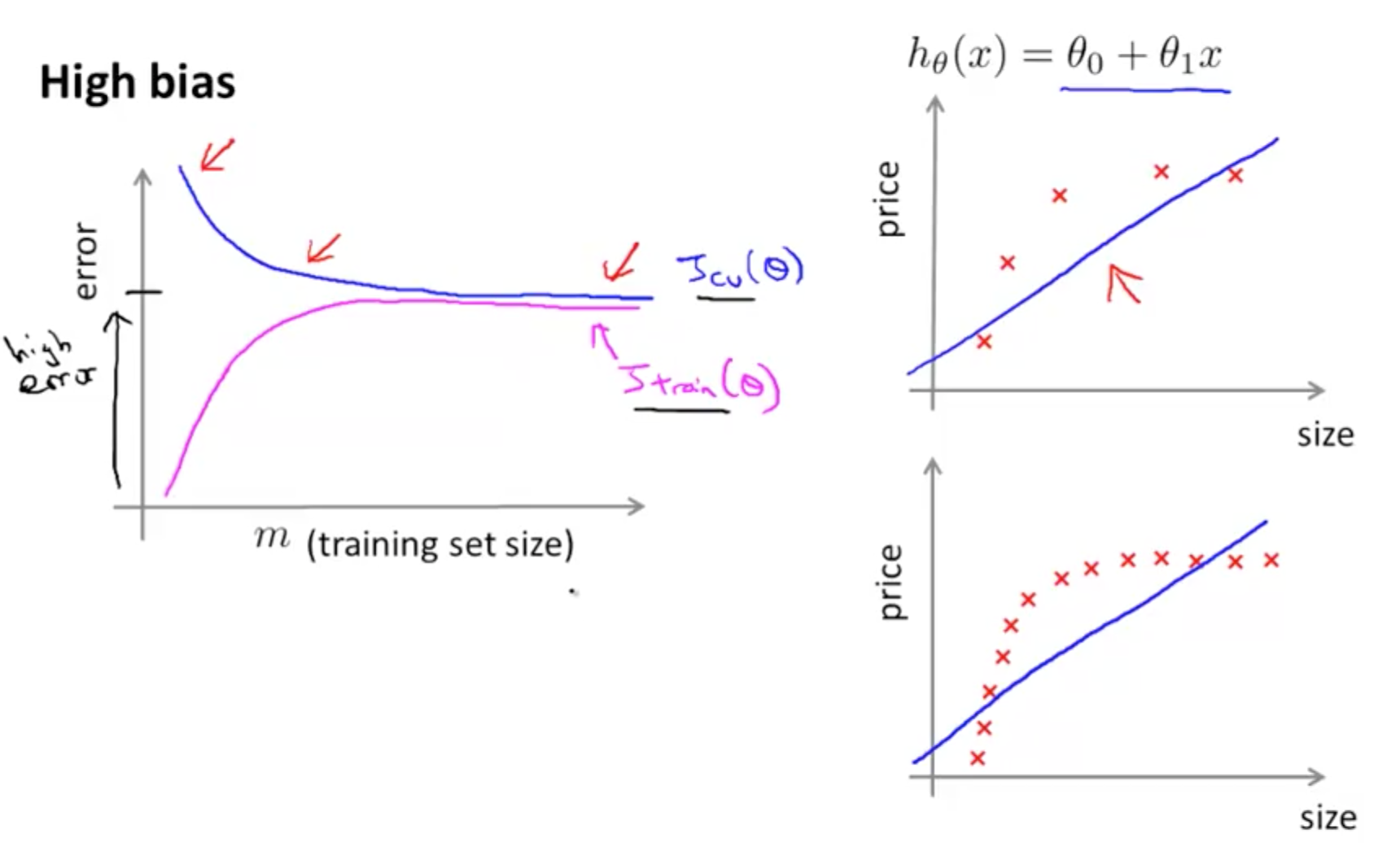
Bad Learning Curve: High Bias
- When training and testing errors converge and are high
  - No matter how much data we feed the model, the model cannot represent the underlying relationship and has high systematic errors
  - Poor fit
  - Poor generalization
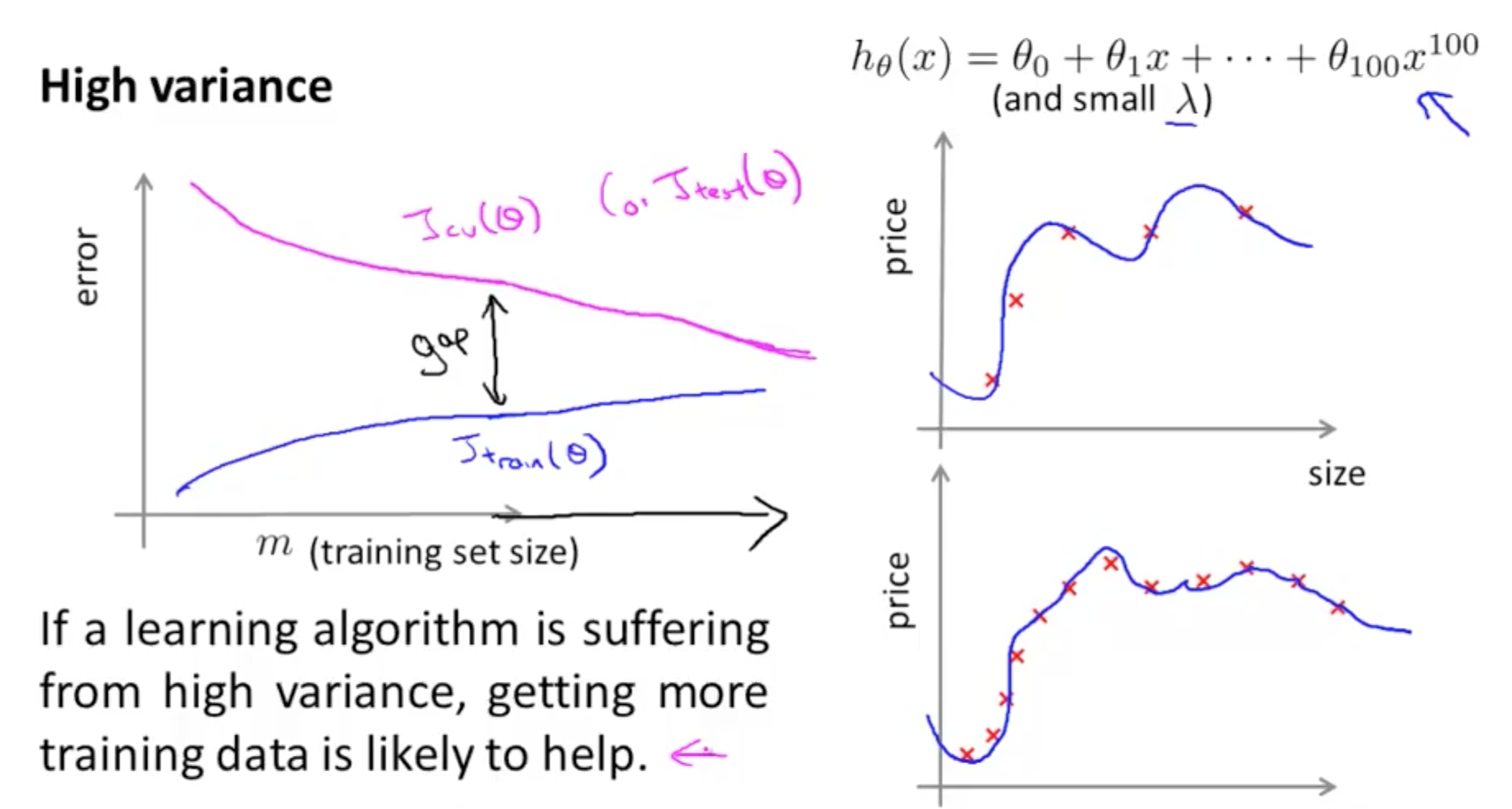
Bad Learning Curve: High Variance
- When there is a large gap between the errors
  - Require data to improve
  - Can simplify the model with fewer or less complex features
Ideal Learning Curve
- Model that generalizes to new data
- Testing and training learning curves converge at similar values
- Smaller the gap, the better our model generalizes

Example 1: High Bias

In this example, you'll see that we'll be using a linear learner on quadratic data
The result is that we've high bias
We'll have a low score (high error)

# imports
from sklearn.linear_model import LinearRegression
from sklearn.learning_curve import learning_curve
import matplotlib.pyplot as plt
from sklearn.metrics import explained_variance_score, make_scorer
from sklearn.cross_validation import KFold
import numpy as np

size = 1000
cv = KFold(size, shuffle=True)

Create X array

#np.reshape(old_shape, new_shape)

# new array (-1, 1)
# -1 implies to take shape from original, hence 1000
# this creates a 1000 x 1 array
X = np.reshape(np.random.normal(scale=2,size=size),(-1,1))
X.shape

(1000, 1)

# np.random.normal(scale=2,size=size) creates a 1000 x 1 matrix
# scale=2 is the standard deviation of the distribution
np.random.normal(scale=2,size=size).shape

(1000,)

Create y array

y = np.array([[1 - 2*x[0] +x[0]**2] for x in X])
y.shape

(1000, 1)

Plot learning curve

def plot_curve():
    # instantiate
    lg = LinearRegression()

    # fit
    lg.fit(X, y)
    
    
    """
    Generate a simple plot of the test and traning learning curve.

    Parameters
    ----------
    estimator : object type that implements the "fit" and "predict" methods
        An object of that type which is cloned for each validation.

    title : string
        Title for the chart.

    X : array-like, shape (n_samples, n_features)
        Training vector, where n_samples is the number of samples and
        n_features is the number of features.

    y : array-like, shape (n_samples) or (n_samples, n_features), optional
        Target relative to X for classification or regression;
        None for unsupervised learning.

    ylim : tuple, shape (ymin, ymax), optional
        Defines minimum and maximum yvalues plotted.

    cv : integer, cross-validation generator, optional
        If an integer is passed, it is the number of folds (defaults to 3).
        Specific cross-validation objects can be passed, see
        sklearn.cross_validation module for the list of possible objects

    n_jobs : integer, optional
        Number of jobs to run in parallel (default 1).
        
    x1 = np.linspace(0, 10, 8, endpoint=True) produces
        8 evenly spaced points in the range 0 to 10
    """
    
    train_sizes, train_scores, test_scores = learning_curve(lg, X, y, n_jobs=-1, cv=cv, train_sizes=np.linspace(.1, 1.0, 5), verbose=0)

    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    plt.figure()
    plt.title("RandomForestClassifier")
    plt.legend(loc="best")
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    plt.gca().invert_yaxis()
    
    # box-like grid
    plt.grid()
    
    # plot the std deviation as a transparent range at each training set size
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1, color="g")
    
    # plot the average training and test score lines at each training set size
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
    
    # sizes the window for readability and displays the plot
    # shows error from 0 to 1.1
    plt.ylim(-.1,1.1)
    plt.show()

%matplotlib inline
plot_curve()

Compared to the theory we covered, here our y-axis is 'score', not 'error', so the higher the score, the better the performance of the model.

Training score (red line) decreases and plateau
- Indicates underfitting
- High bias
Cross-validation score (green line) stagnating throughout
- Unable to learn from data
Low scores (high errors)
- Should tweak model (perhaps increase model complexity)

Example 2: High Variance

Noisy data and complex model

There're no inline notes here as the code is exactly the same as above and are already well explained.

from sklearn.tree import DecisionTreeRegressor

X = np.round(np.reshape(np.random.normal(scale=5,size=2*size),(-1,2)),2)
y = np.array([[np.sin(x[0]+np.sin(x[1]))] for x in X])

def plot_curve():
    # instantiate
    dt = DecisionTreeRegressor()

    # fit
    dt.fit(X, y)
    
    
    """
    Generate a simple plot of the test and traning learning curve.

    Parameters
    ----------
    estimator : object type that implements the "fit" and "predict" methods
        An object of that type which is cloned for each validation.

    title : string
        Title for the chart.

    X : array-like, shape (n_samples, n_features)
        Training vector, where n_samples is the number of samples and
        n_features is the number of features.

    y : array-like, shape (n_samples) or (n_samples, n_features), optional
        Target relative to X for classification or regression;
        None for unsupervised learning.

    ylim : tuple, shape (ymin, ymax), optional
        Defines minimum and maximum yvalues plotted.

    cv : integer, cross-validation generator, optional
        If an integer is passed, it is the number of folds (defaults to 3).
        Specific cross-validation objects can be passed, see
        sklearn.cross_validation module for the list of possible objects

    n_jobs : integer, optional
        Number of jobs to run in parallel (default 1).
        
    x1 = np.linspace(0, 10, 8, endpoint=True) produces
        8 evenly spaced points in the range 0 to 10
    """
    
    train_sizes, train_scores, test_scores = learning_curve(dt, X, y, n_jobs=-1, cv=cv, train_sizes=np.linspace(.1, 1.0, 5), verbose=0)

    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    plt.figure()
    plt.title("RandomForestClassifier")
    plt.legend(loc="best")
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    plt.gca().invert_yaxis()
    
    # box-like grid
    plt.grid()
    
    # plot the std deviation as a transparent range at each training set size
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1, color="g")
    
    # plot the average training and test score lines at each training set size
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
    
    # sizes the window for readability and displays the plot
    # shows error from 0 to 1.1
    plt.ylim(-.1,1.1)
    plt.show()

plot_curve()

Compared to the theory we covered, here our y-axis is 'score', not 'error', so the higher the score, the better the performance of the model.

Training score (red line) is at its maximum regardless of training examples
- This shows severe overfitting
Cross-validation score (green line) increases over time
Huge gap between cross-validation score and training score indicates high variance scenario
- Reduce complexity of the model or gather more data