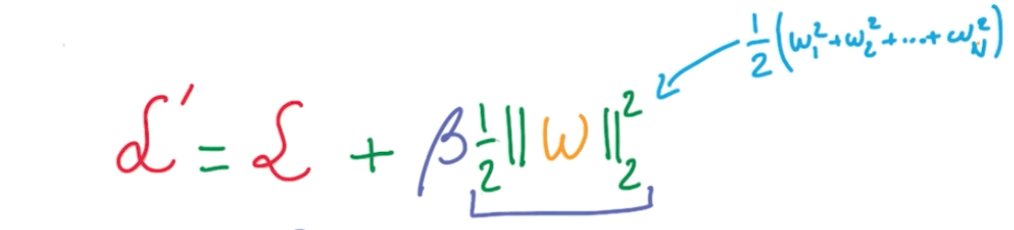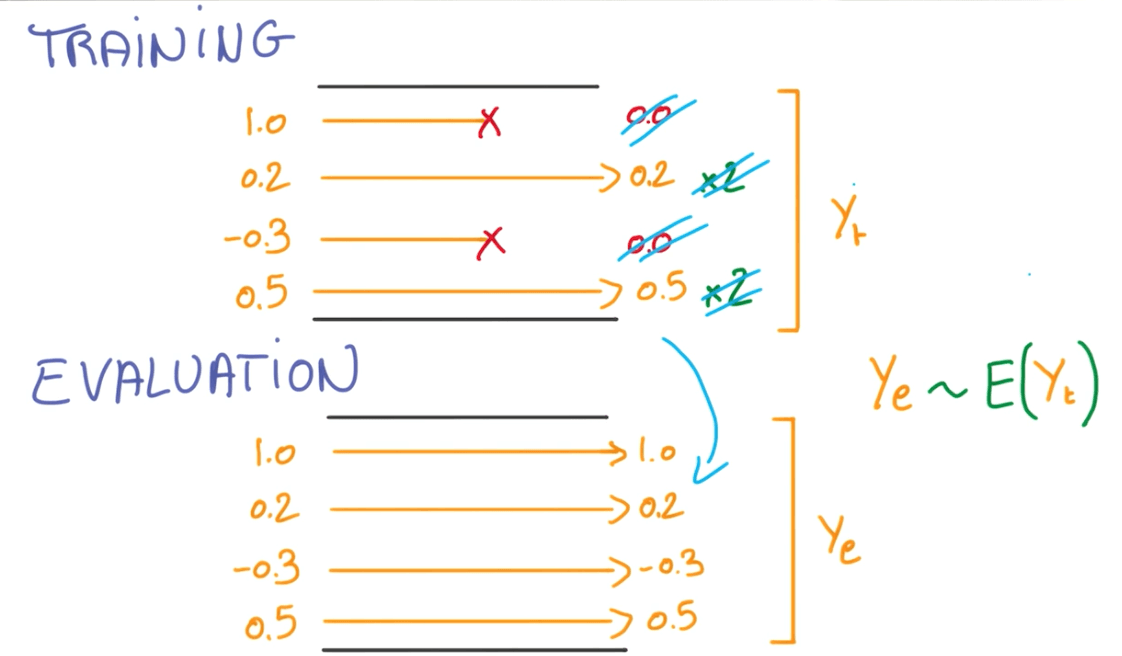Build a deep neural network with ReLUs and Softmax.
Deep Neural Networks: Introduction¶
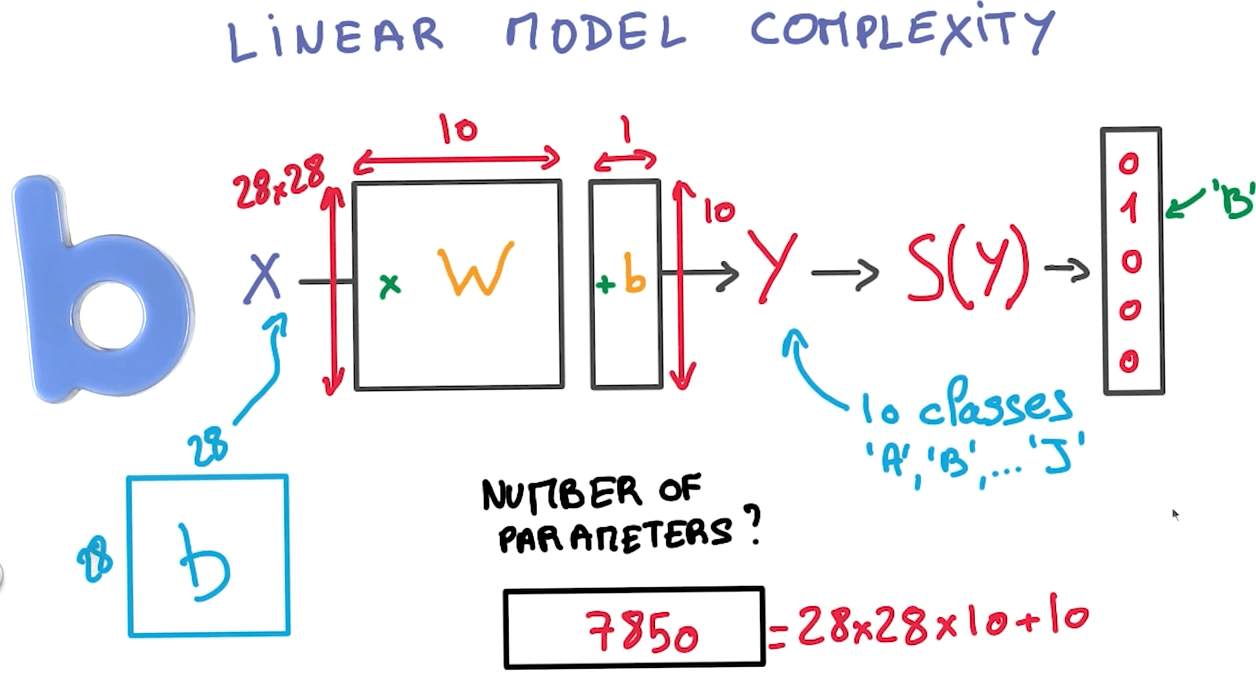
Linear Model Complexity
- If we have N inputs and K outputs, we would have:
- (N+1)K parameters
- Limitation
- $y = x_1 + x_2$ can be represented well
- $y = x_1 * x_2$ cannot be represented well
- Benefits
- Derivatives are constants
Rectified Linear Units (ReLUs)
- This is a non-linear function.
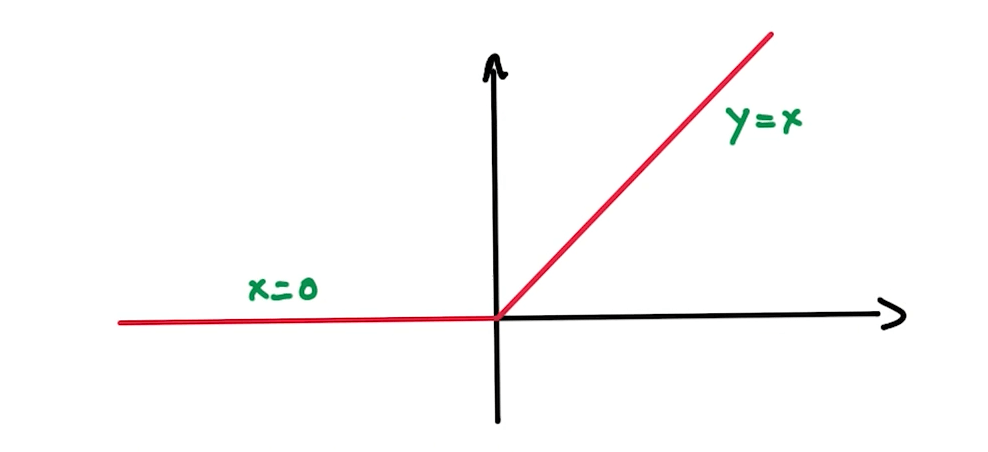
- Derivatives are nicely represented too.
- Derivatives are nicely represented too.
Network of ReLUs: Neural Network
- We can do a logistic classifier and insert a ReLU to make a non-linear model.
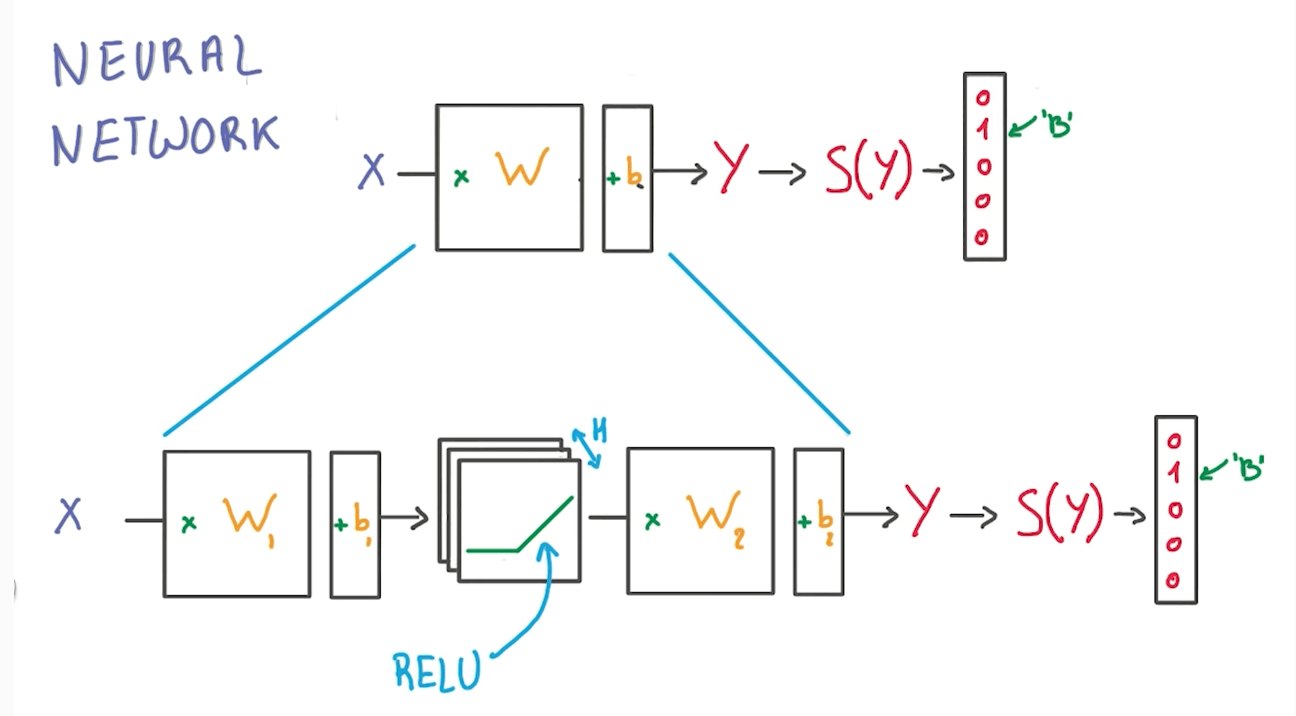
- H: number of RELU units
2-Layer Neural Network
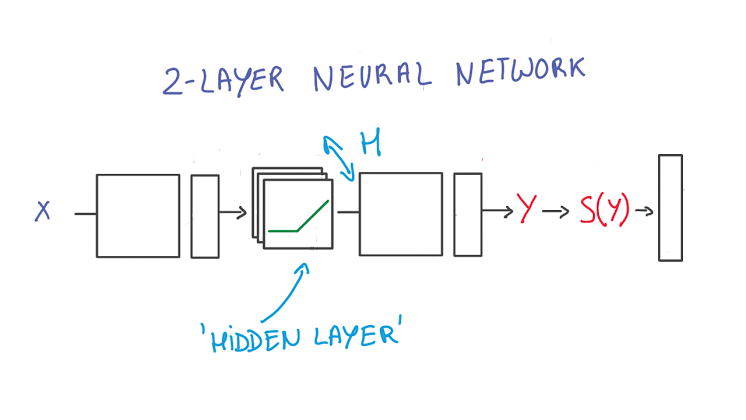
- The first layer effectively consists of the set of weights and biases applied to X and passed through ReLUs. The output of this layer is fed to the next one, but is not observable outside the network, hence it is known as a hidden layer.
- The second layer consists of the weights and biases applied to these intermediate outputs, followed by the softmax function to generate probabilities.
- A softmax regression has two steps: first we add up the evidence of our input being in certain classes, and then we convert that evidence into probabilities.
Stacking Simple Operations
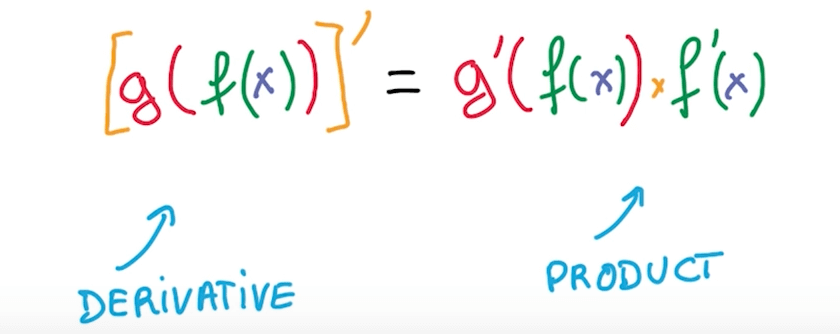
- We can compute derivative of function by taking product of derivatives of components.
Backpropagation

- Forward-propagation
- You will have data X flowing through your NN to produce Y.
- Back-propagation
- Your labelled data Y flows backward to calculate "errors" of our calculations.
- You will be calculating the gradients ("errors"), multiply it by a learning rate, and use it to update our weights.
- We will be doing this many times.
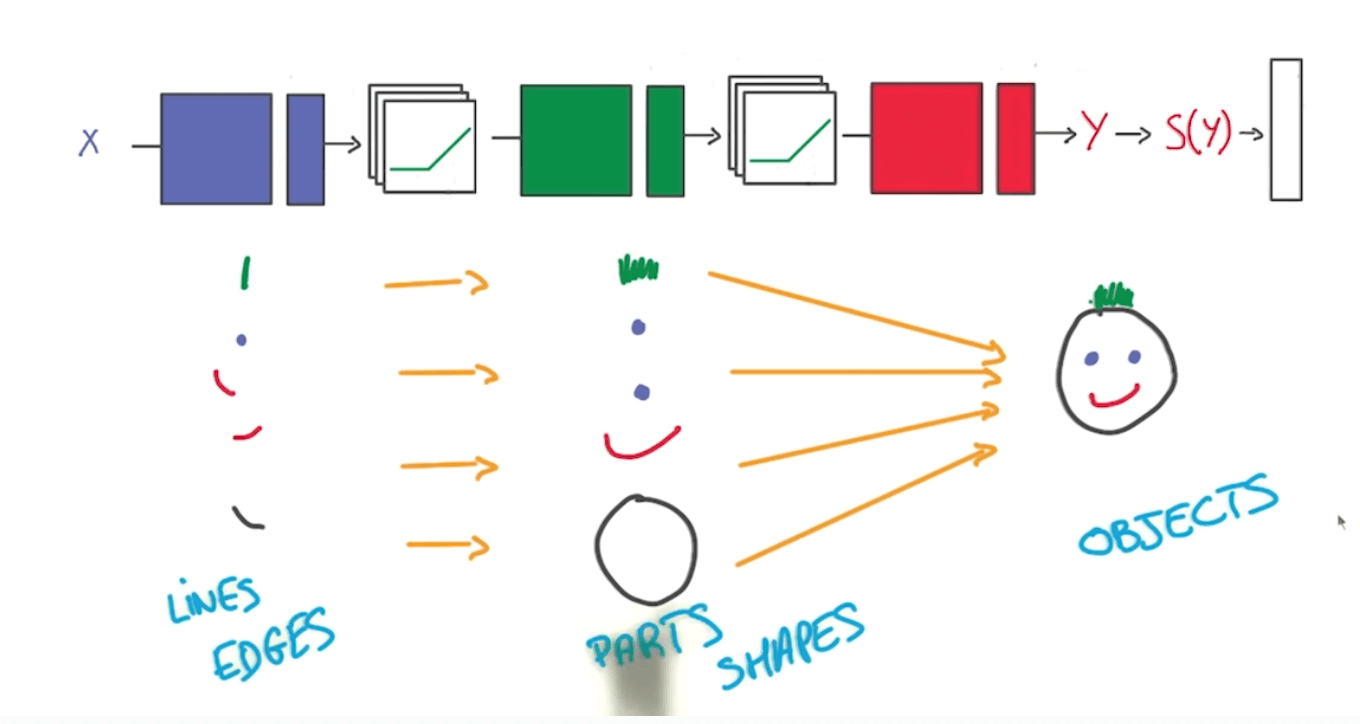
Go Deeper
- It is better go deeper than increasing the size of the hidden layers (by adding more nodes)
- It gets hard to train.
- We should go deeper by adding more hidden layers.
- You would reap parameter efficiencies.
- However you need large datasets.
- Also, deep models can capture certain structures well such as the following.
Regularization
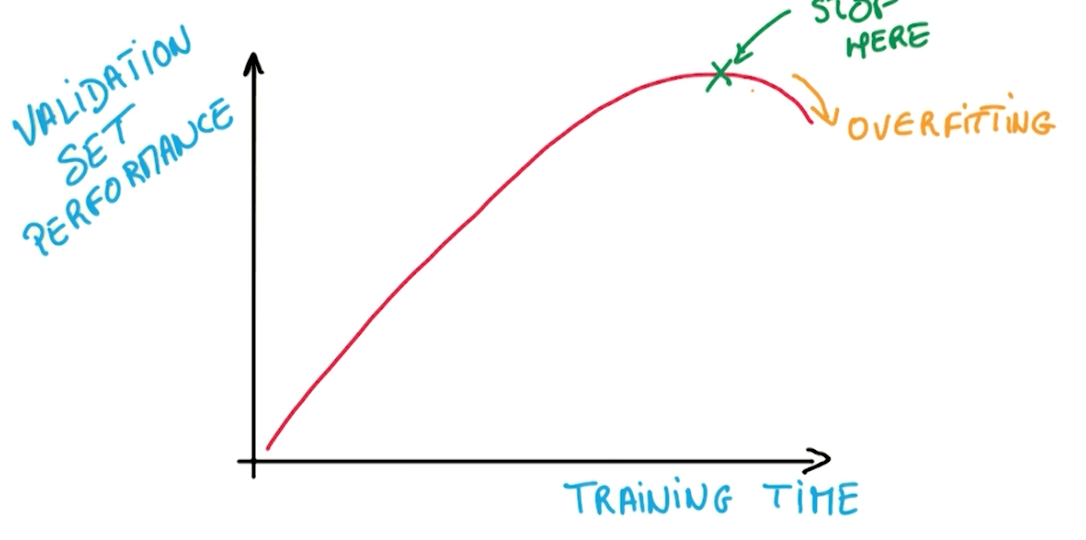
- We normally train networks that are bigger than our data.
- Then we try to prevent overfitting with 2 methods.
- Early termination
- Regularization
- Applying artificial constraints.
- Implicitly reduce number of free parameters while enabling us to optimize.
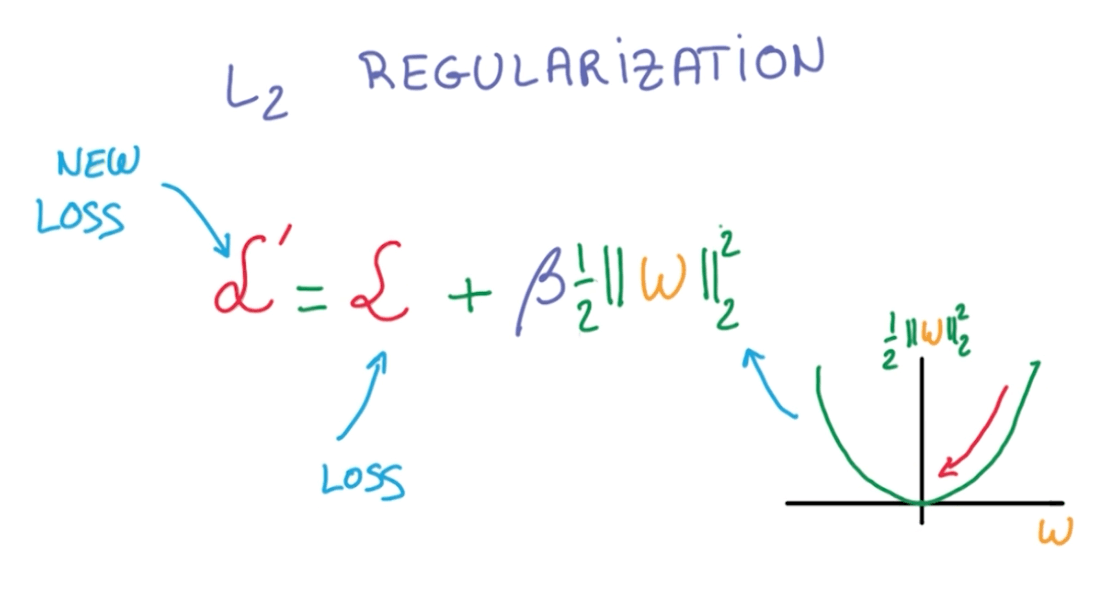
- L2 Regularization
- We add another term to the loss that penalizes large weights.
- This is simple because we just add to our loss.
- Early termination
- Then we try to prevent overfitting with 2 methods.
L2 Regularization's Derivative
- The norm of w is the sum of squares of the elements in the vector.
- The equation:
- The derivative:
- $ (\frac {1}{2} w^2)' = w $
- The equation:
L2 Regularizatin: Dropout
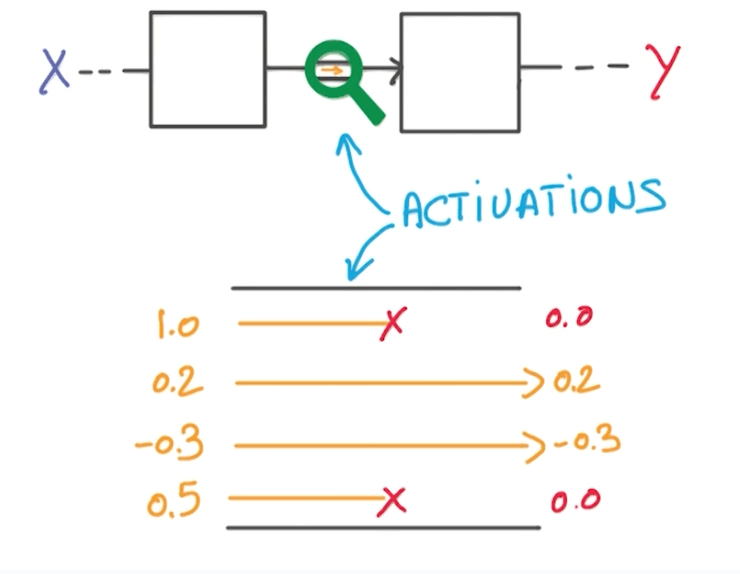
- Your input goes through an activation function.
- During the activation function, we randomly take half of the data and set to 0.
- We do this multiple times.
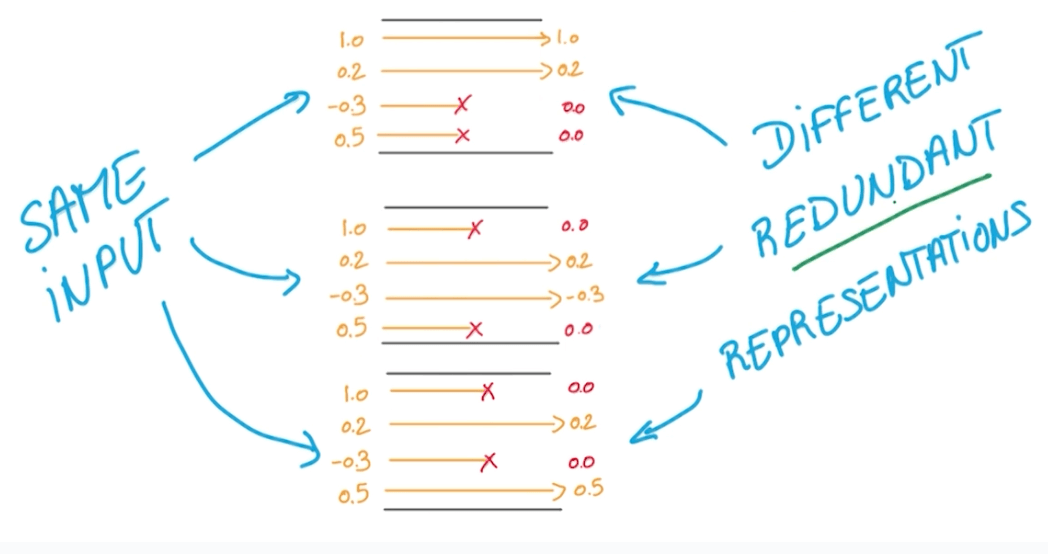
- We are forced to learn redundant information.
- It's like a game of whack-a-mole.
- There's always one or more that represents the same thing.
- Benefits
- It prevents overfitting.
- It makes network act like it's taking a consensus of an ensemble of networks.
Dropout during Evaluation
- We would take the expectation of our training y's.