Deep convnets for image recognition
Deep Convolutional Networks

Convolutional Neural Nets: Introduction

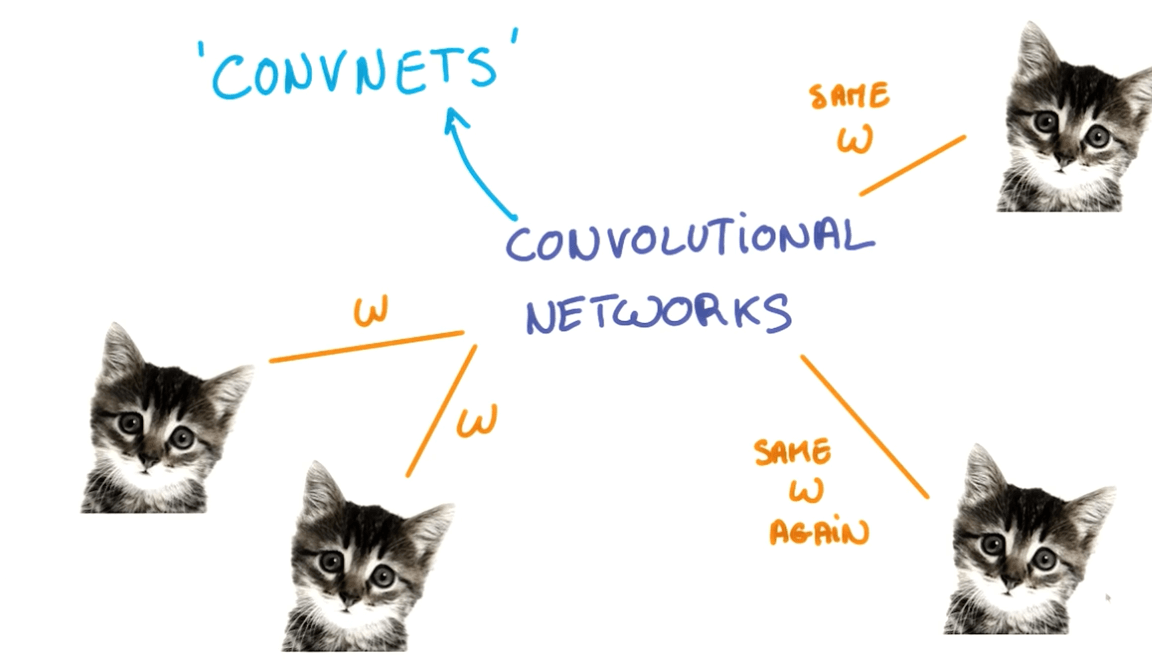
Translation Invariance

  • Image
    • Different positions
    • Same objects
  • Text
    • Kitten in a long text
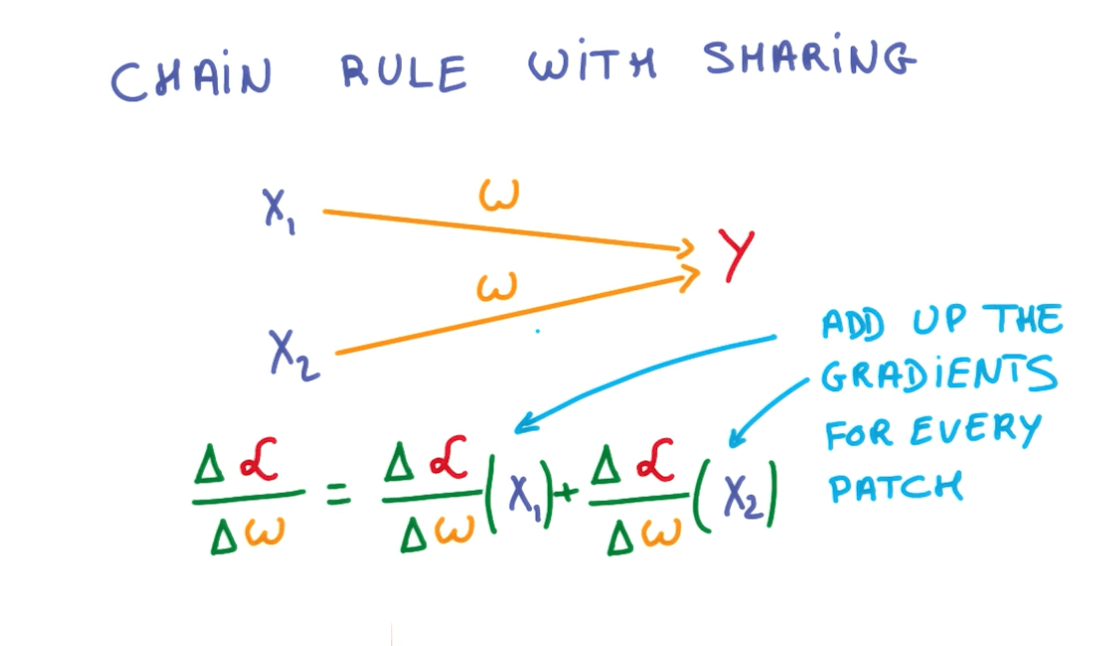
    • You can use weight sharing and train them jointly for those inputs

Convnets

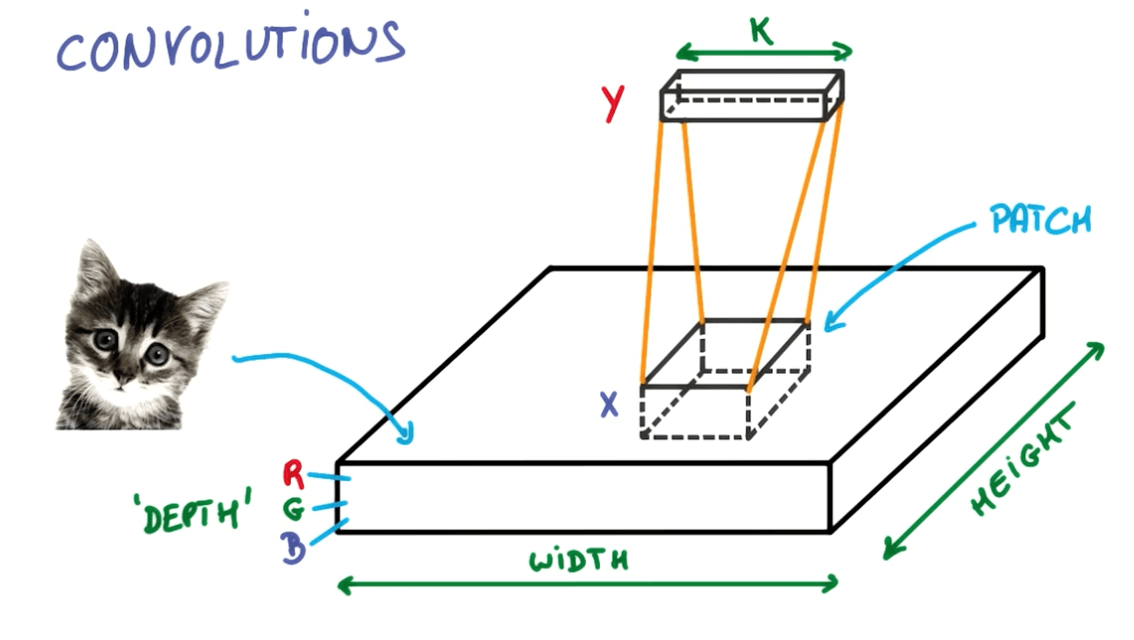
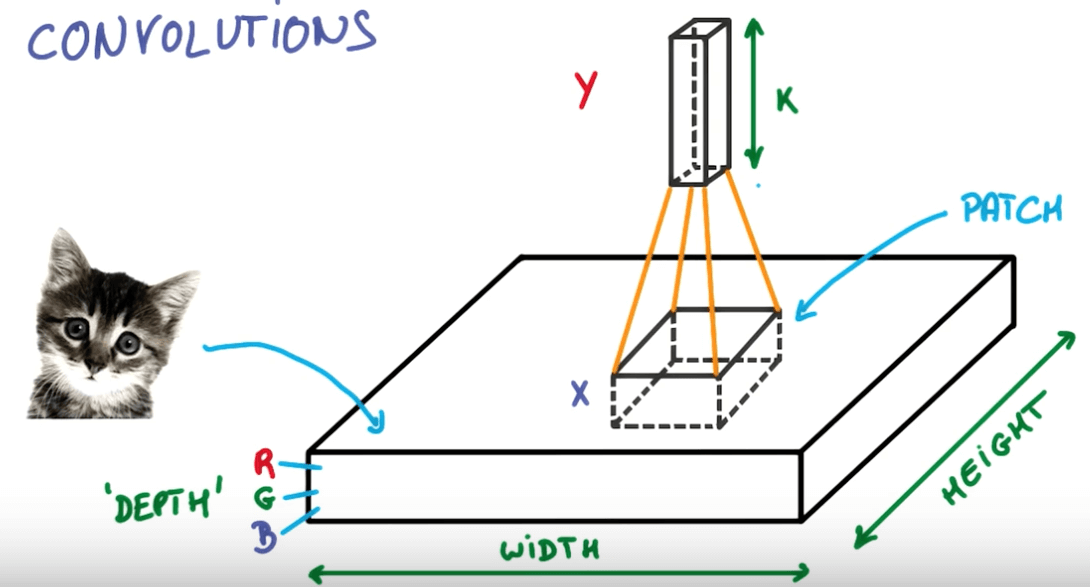
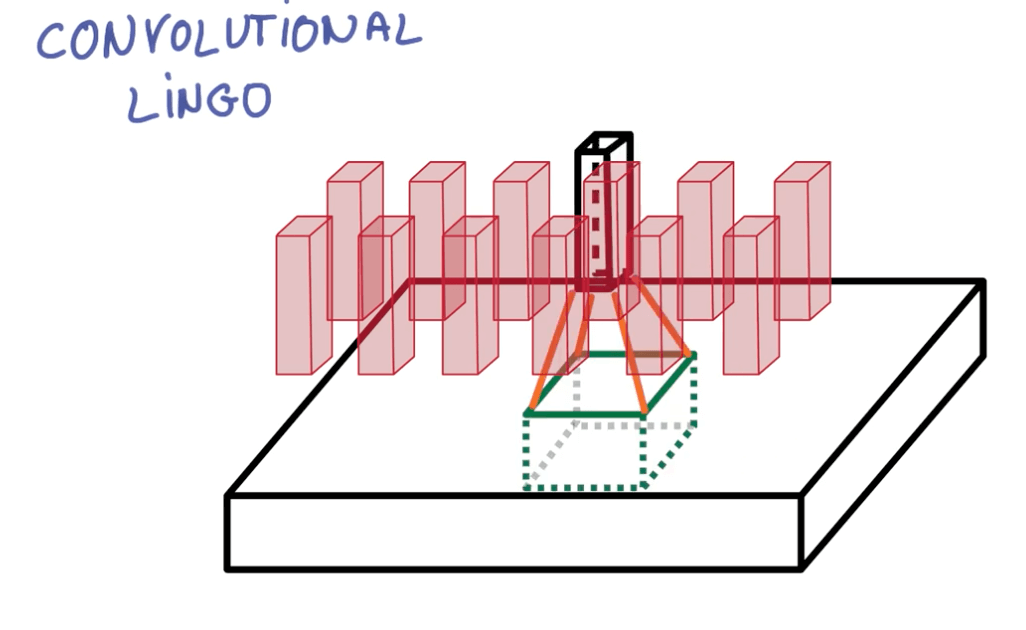
  • Neural networks that share their parameters across space
  • We take a portion of the image and run a neural network.
  • We then slide the neural network across the image
    • Here you can see we've a layer that has a deeper depth but smaller space.
    • We will slide the neural network on this layer that will again increase the depth and reduce the space.
    • We continue to do this until we've reached a stage of maximum depth k where k are the outputs we want.
  • Instead of having stacks of matrix multipliers, we would have stacks of convolutions.
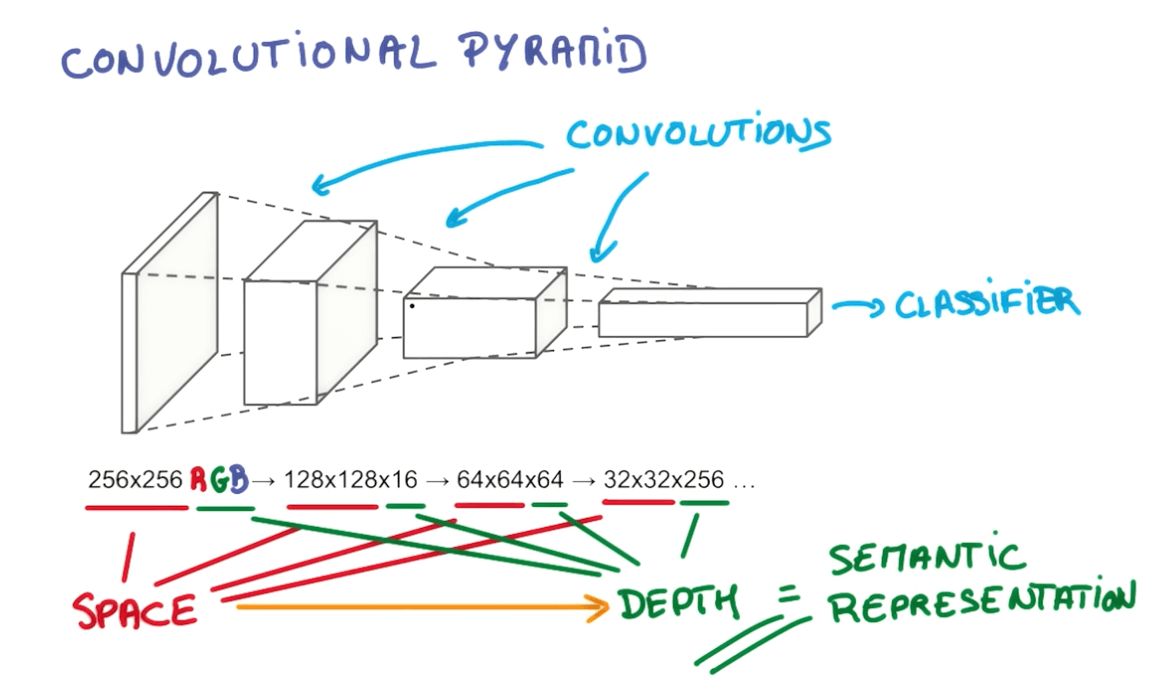
      • Here you can see we're trying to reduce the space and increase the depth.

Convnets Terms

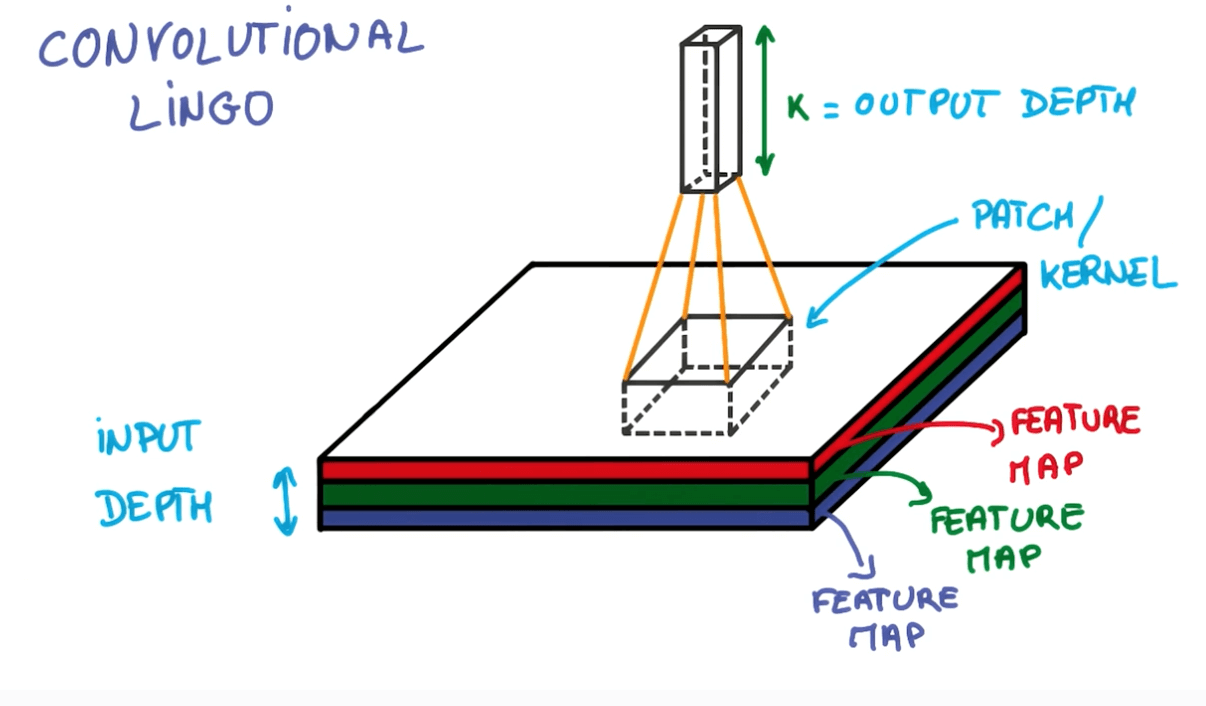
  • Strides
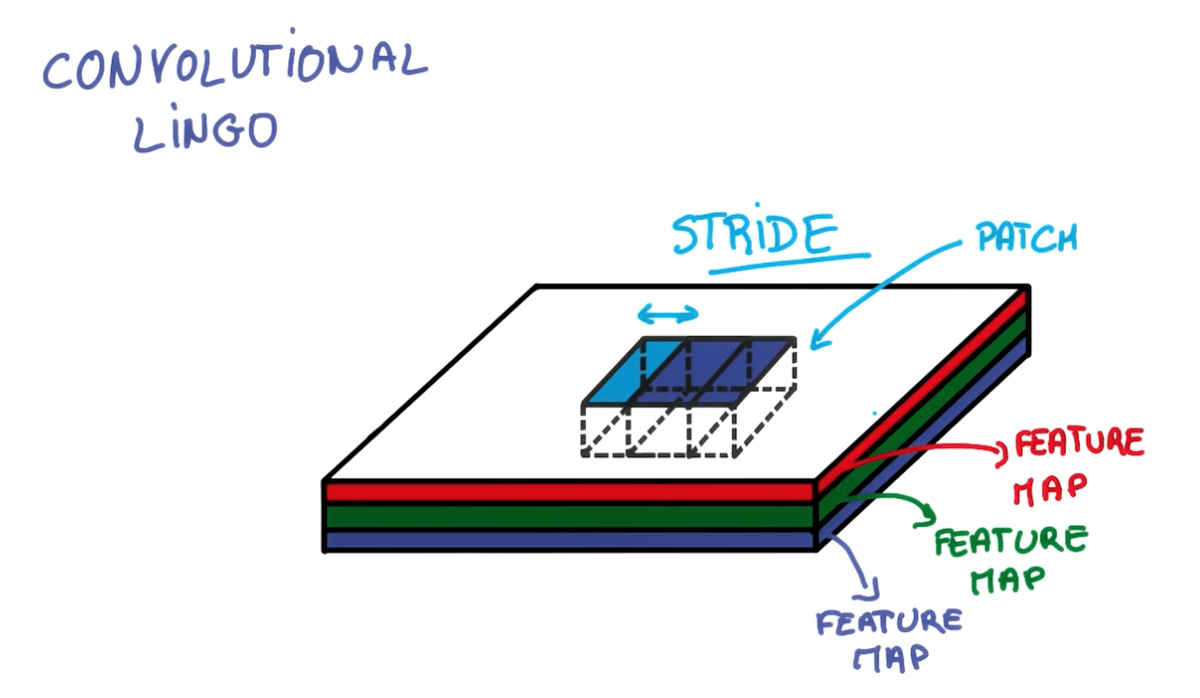
      • Where stride is the number of pixels that we are shifting.
      • Stride: 1
        • Output same size as input
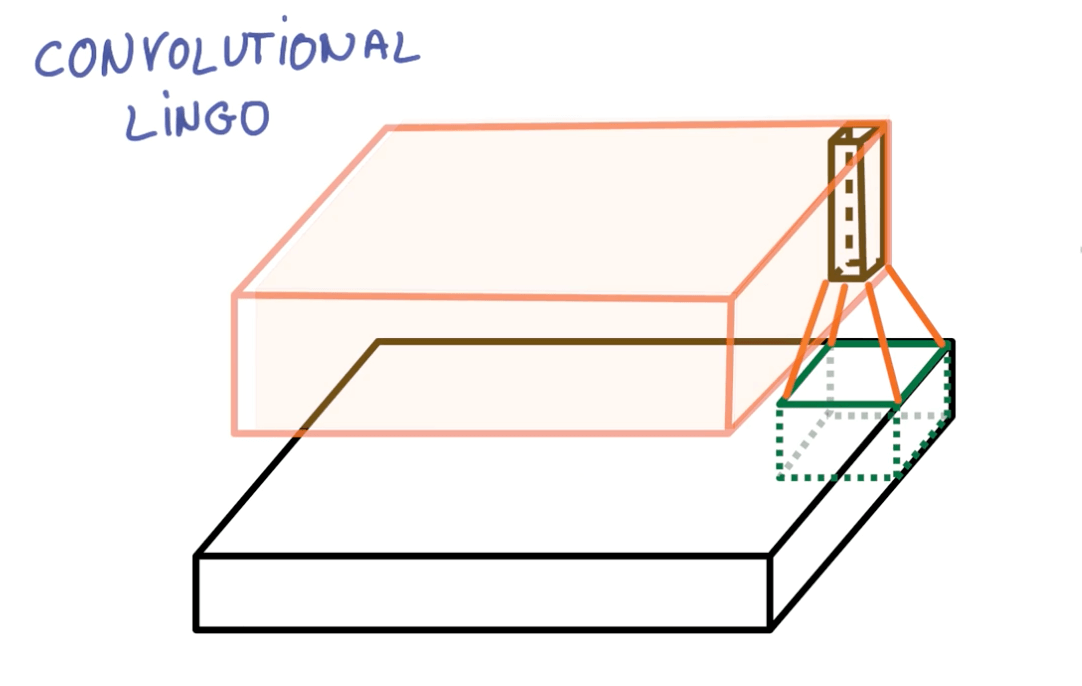
      • Stride: 2
        • Output roughly half the size
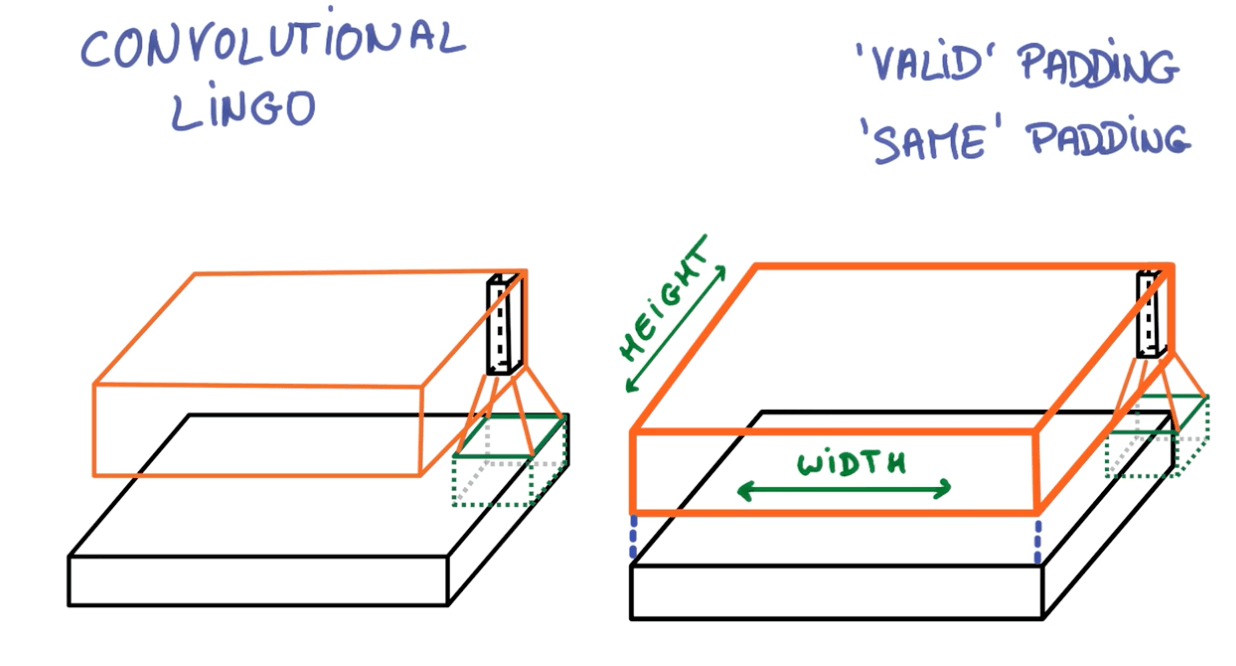
  • Paddings
    • Left: valid padding
    • Right: same padding

Strides, depth and padding

  • Imagine you have 28x28 image.
  • You run a 3x3 convolution on it.
    • Input depth: 3
    • Output depth: 8
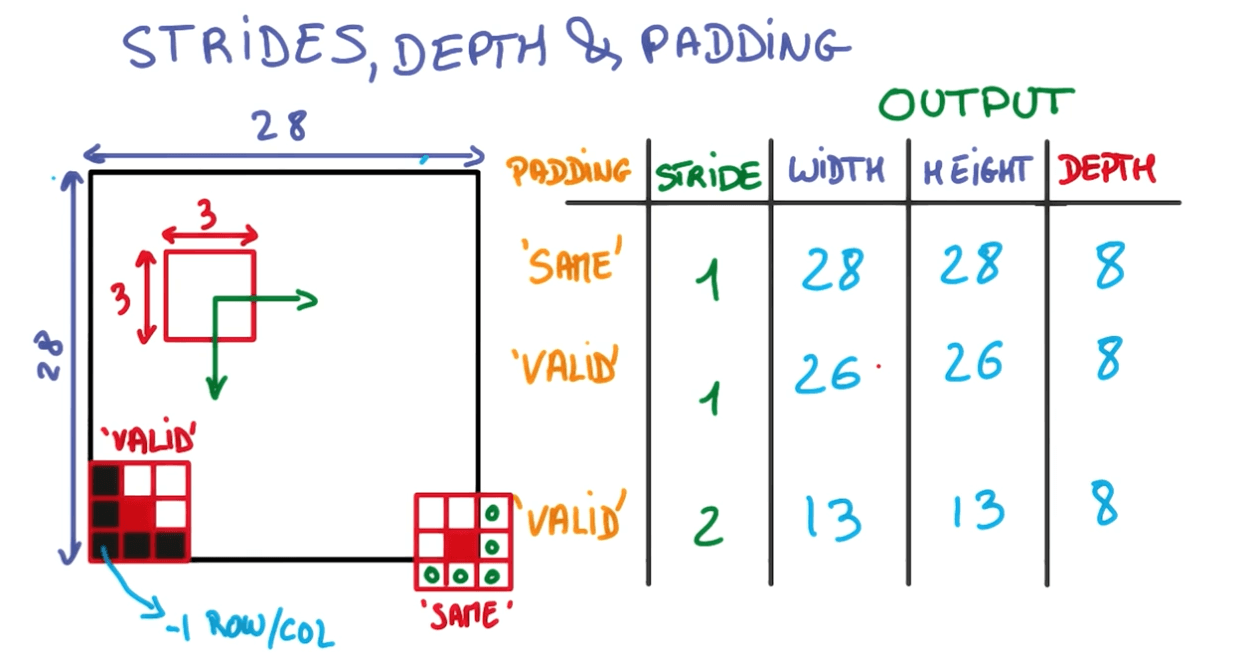
    • For stride: 1 and padding: same (1)
      • You would have the exact same dimensions.
      • You would be taking a F x F x D_input dot-product to come up with a number.
    • For stride: 1 and padding: valid (0)
      • You would have one less row and column
    • For stride: 2 and padding: valid (0)
      • You would have half the output.

Calculating Output Size

  • $O = \frac {W - K - 2P} {S} + 1 $
    • O is the output height/length
    • W is the input height/length
    • K is the filter size (kernel size)
    • P is the padding
    • S is the stride

Padding Size

  • In general it's common to see same (zero) padding, stride 1 and filters of size FxF.
  • Zero-padding = $\frac {F - 1}{2}$
    • If you do not pad (same padding), you would decrease the width and height of your layers gradually.
      • This might not be something you want.

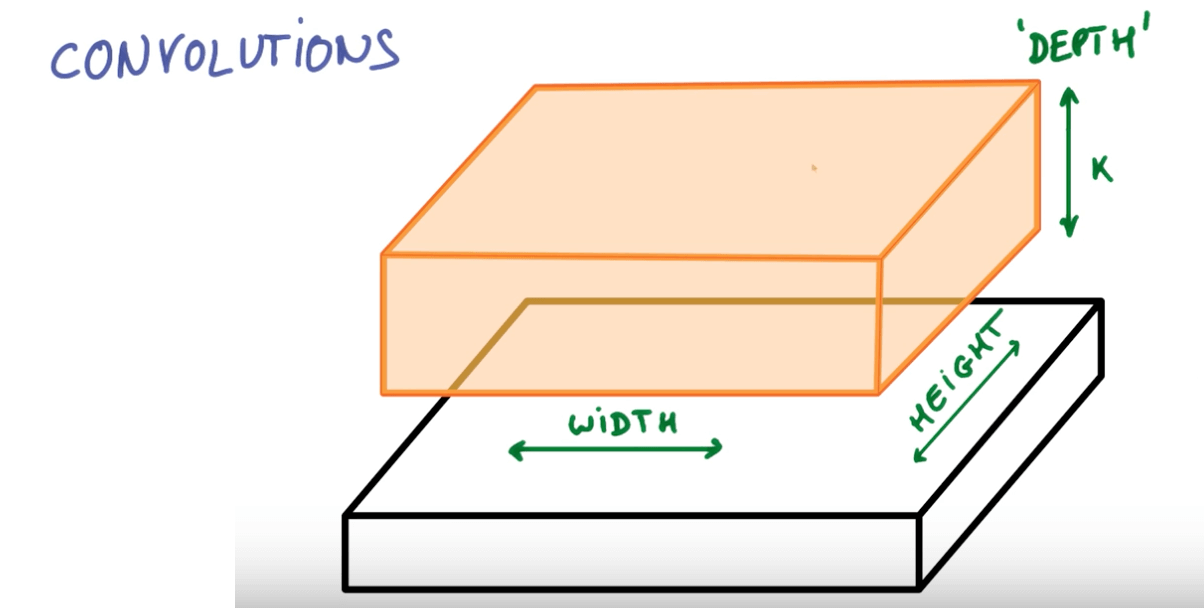
Depth

  • Number of filters = depth.
  • We try to keep this in powers of two.
    • 32, 64, 128, 512 etc.
    • This is for computational reasons.

Number of Parameters

  • Number of parameters in layer = (F x F x D_input + 1) x D_filter
    • Where F is the filter size
    • D_input is the depth of the input layer
    • 1 is the bias
    • D_filter is the depth of the filter
    • Parameters per filter: (F x F x D_input + 1)

Convolution Networks

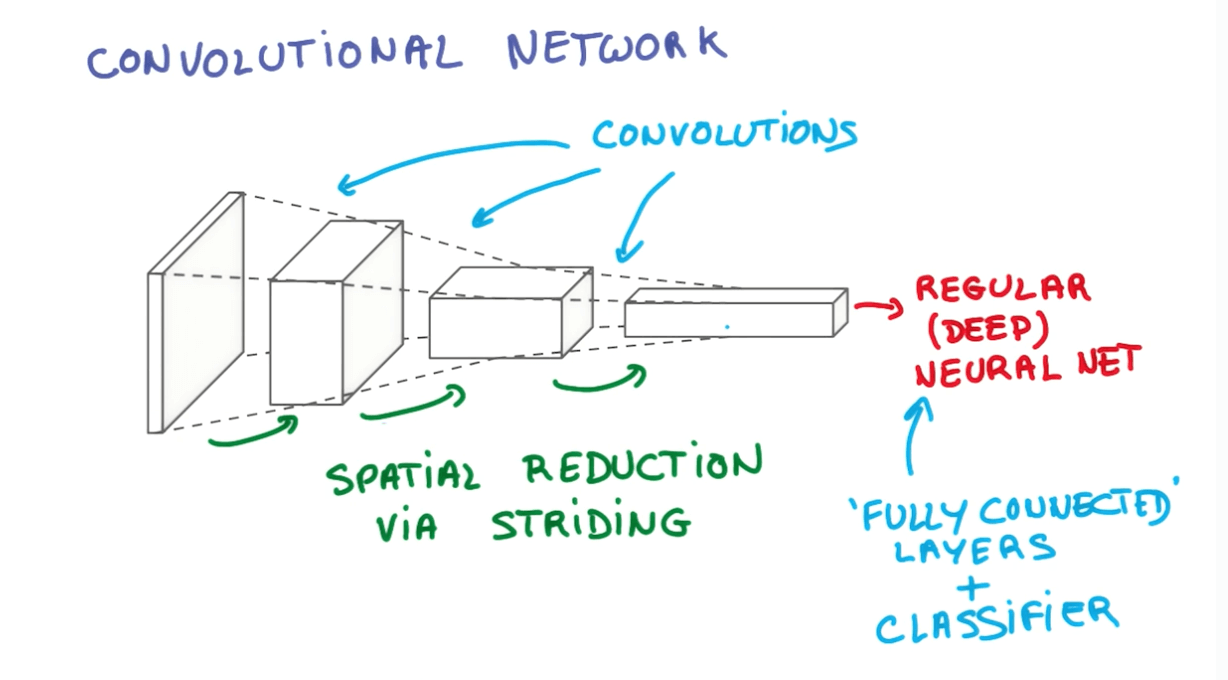
    • Fully Connected (FC) Layer
      • Basically it connects to the entire input volume like a neural network.
      • Final layer after we have done all our convolutions.
    • ReLU Layers
      • Remember there are ReLU Layers after every Conv and FC.

Advanced convnet-ology

  • Pooling
  • 1 x 1 convolutions
  • Inception

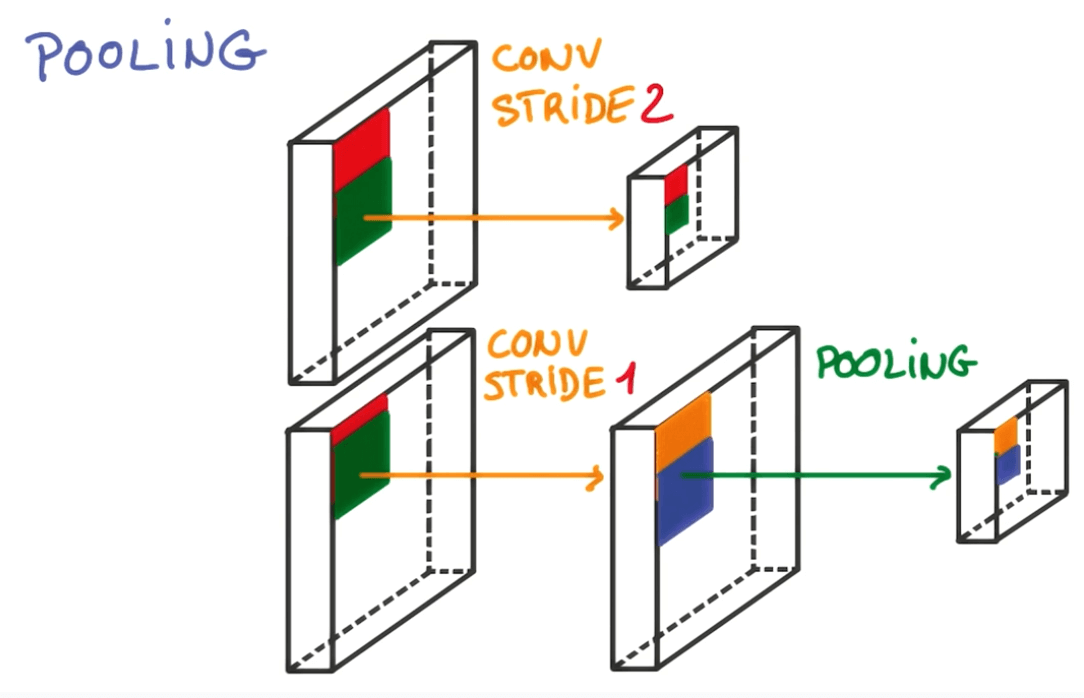
Pooling

  • Striding
    • We shift the filter by a few pixel each time.
    • This is very aggressive method that removes a lot of information.
  • Pooling
    • We can take a smaller stride.
    • Take all the convolutions in the neighbors.
    • Combine them somehow, and this is called pooling.
      • We will be preserving the depth.
      • But we will be reducing the width and height.
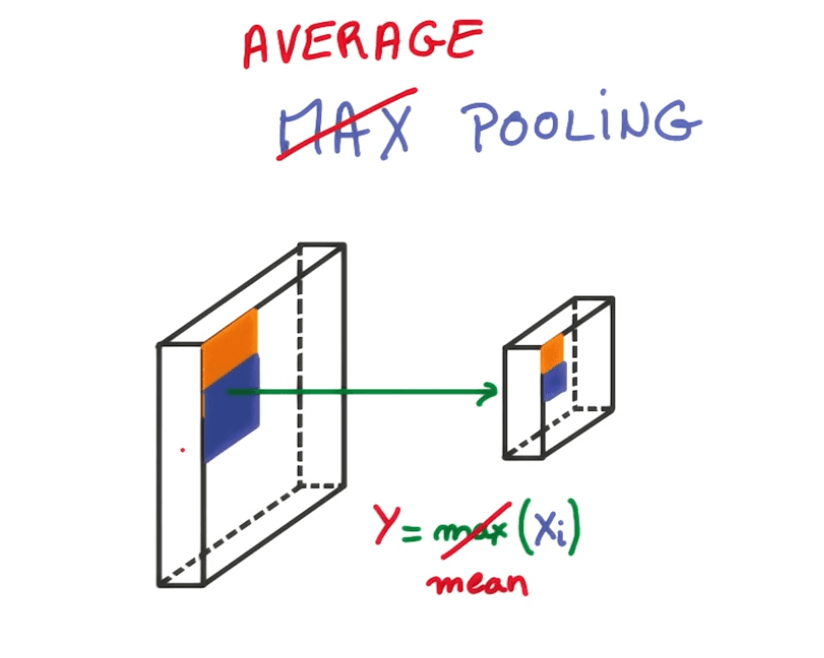
    1. Max Pooling
      • At every point in a feature map, look at a small neighborhood around that point and compute the maximum of all the responses around it.
      • Typical architecture
    1. Average pooling
      • Instead oftaking the max, we take the average.
      • It's similar to taking a blurred, low-resolution, view of the feature map.

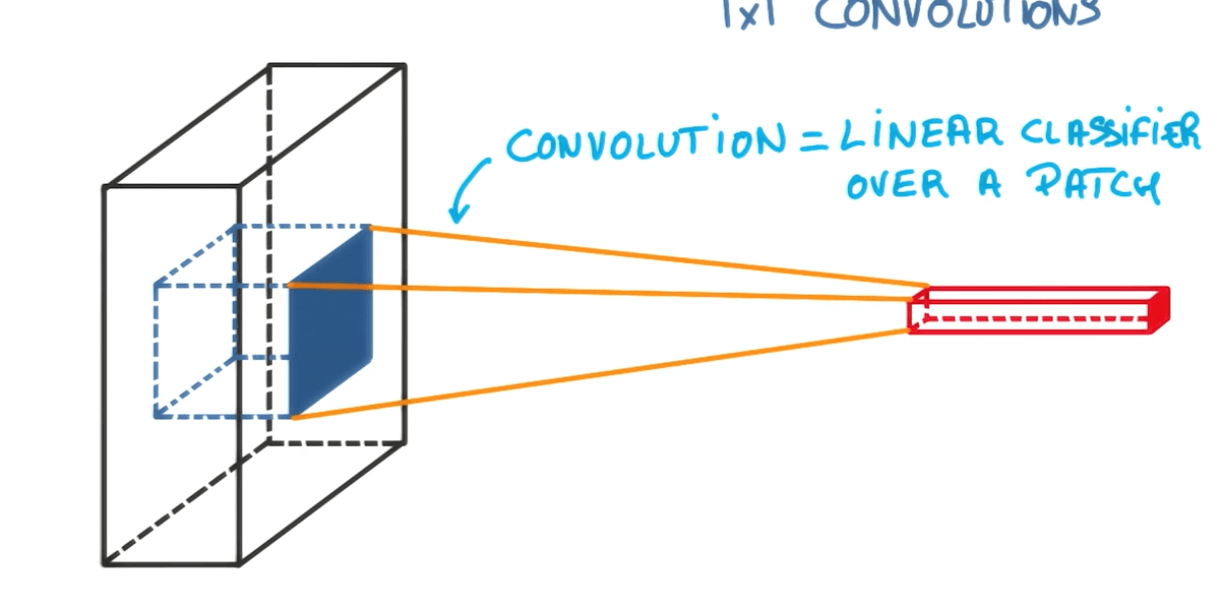
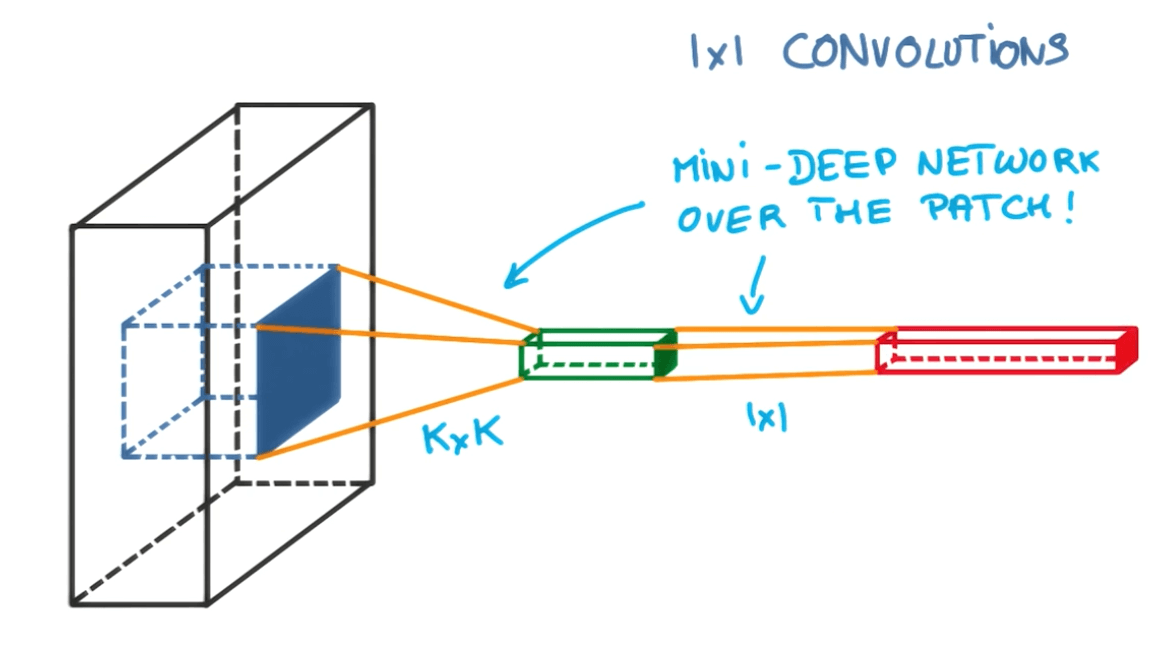
1x1 Convolutions

  • Here we are using only 1 pixel by 1 pixel.
  • Traditional.
  • Now we add a 1x1 convolution.

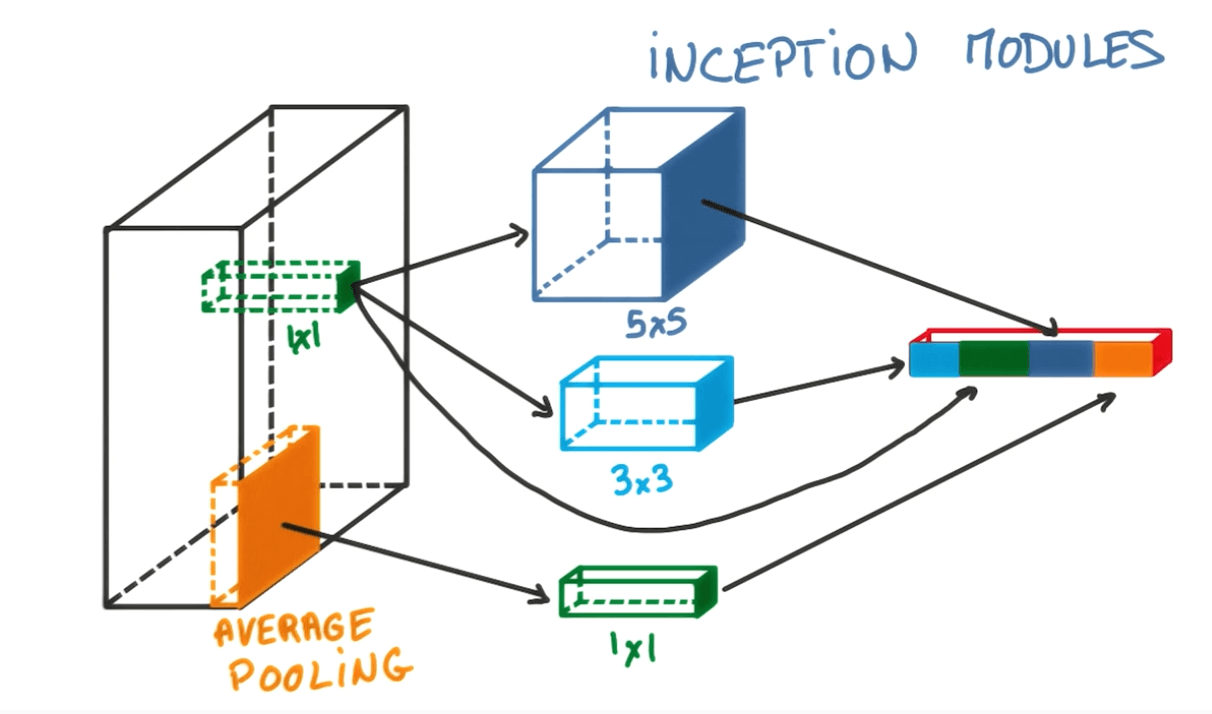
Inception Module

  • This is like an ensemble of methods.

Evaluation of results

  • We can use accuracy to evaluate the predicted values and our labels.
  • But a better method would be to use the top-1 and top-5 errors.

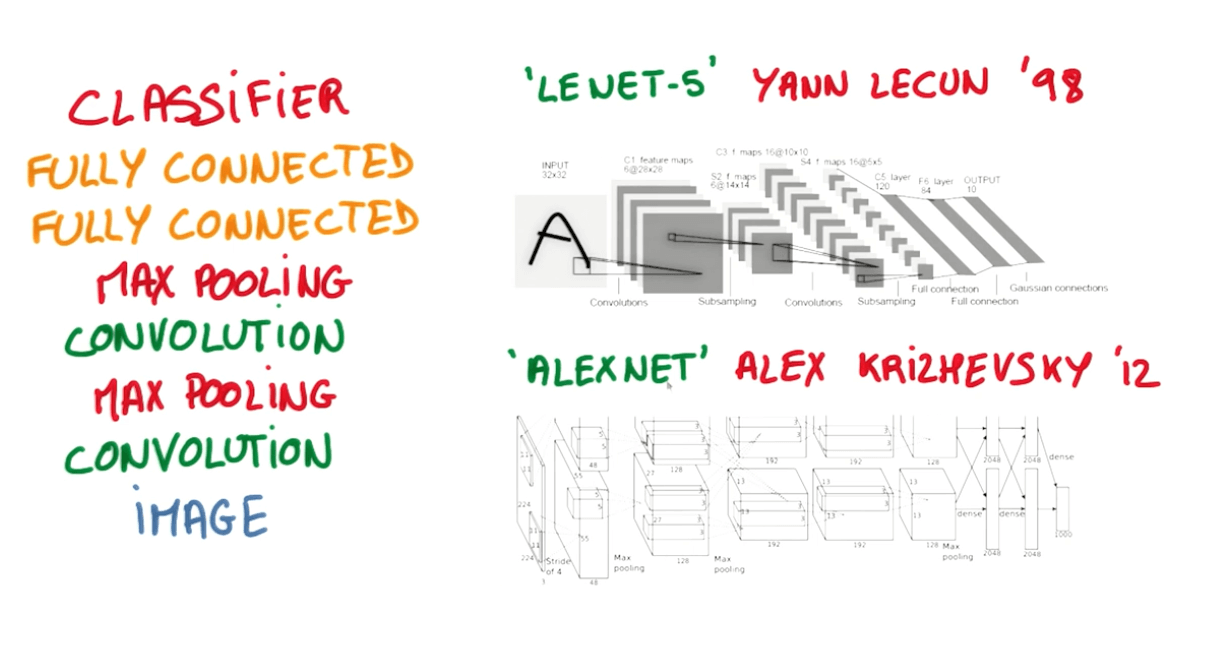
Progress in Convs (in order of lower top-1 and top-5 errors)

  • LeNet-5
  • AlexNet
  • ZFNet
  • VGGNet
  • GoogLeNet
  • ResNet
    • As of September 2016, this is the latest state-of-the-art implementation for convs.

Further Readings

Tags: machine_learning