Spam classifier example, error analysis, skewed data, precision, recall and large data sets.

1. Building a Spam Classifier

I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.

1a. Prioritizing

  • Let’s say you want to build a spam classifier
  • How do you implement supervised learning?
    • We can create the following
      • x = features of email
        • Choose 100 words indicative of spam or not spam
        • In practice is to look through training set and choose most frequently occurring n words (10 000 to 50 000)
      • y = spam (1) or non-spam (0)
      • Example
  • How do you spend your time to have a low error?
    • Collect lots of data
    • Develop sophisticated features based on email routing information (from email header)
    • Develop sophisticated features for message body
      • Should ‘discount’ and ‘discounts’ be treated as the same word?
      • How about ‘deal’ and ‘Dealer’?
      • Punctuation?
    • Develop sophisticated algorithm to detect misspellings
      • med1cine
      • w4tches
      • m0rtage
  • Don’t base on your gut feeling!

1b. Error Analysis

  • Recommended Approach
    • Start with a simple algorithm that you can quickly implement and test it on your cross validation data
    • Plot learning curves to decide if more data, more features, etc. are likely to help
    • Error analysis:
      • Manually examine the examples (in cross validation set) that your algorithm made errors on
      • See if you spot any systematic trend in what type of examples it is making errors on
      • Don’t base anything off your gut feeling!
  • Error Analysis Example
    • m_cv = 500
      • number of cross-validation examples
    • Algorithm misclassified 100 emails
    • Manually examine the 100 errors and categorize them base don
      • What type of email they are
        • Pharma: 12
        • Replica: 4
        • Phishing: 53
        • Other: 31
      • What cues (features) you think would have helped the algorithms classify them correctly
        • Deliberate misspellings: 5
          • m0rtgage
          • med1cine
            • This indicates how there are a small number here
        • Unusual email routing: 16
        • Unusual punctuation: 32
          • This might be worthwhile to spend time to develop sophisticated features
    • This is the reason why we should do a quick and dirty implementation to discover errors and identify areas to focus on
  • Importance of numerical evaluation
    • Should discount, discounts, discounted, discounting etc. be treated as the same word?
      • You can use a “stemming” software, “Porter Stemmer”
      • This would allow you to treat all those variations as the same work
        • Software may mistake universe and university as the same word
      • Error analysis may not be helpful for deciding if this is likely to improve performance
        • The only way is to try it
        • We need a numerical solution (cross validation error)of algorithm’s performance with and without stemming
          • Without stemming: 5%
          • With stemming: 3%
            • This implies that it may be useful to implement stemming
          • Distinguish between upper and lower case: 3.2%
  • Why is the recommended approach to perform error analysis using the cross validation data instead of the test data?
    • If we develop new features by examining the test set, then we may end up choosing features that work well specifically for the test set, so Jtest(θ) is no longer a good estimate of how we generalize to new examples
    • Do error analysis on cross validation set, do not use it on the test set!

2. Handling Skewed Data

2a. Error Metrics for Skewed Classes

  • Consider a problem where you want to find out if someone has cancer
    • y = 1, cancer
    • y = 0, no cancer
    • You train a logistic regression model, h0(x) and you find that you have 1% error on a test set
      • 99% correct diagnosis
    • But only 0.50% of patients have cancer
      • This is a problem of skewed classes
      • This code would have a 0.5% error, lower than your logistic regression model but it’s simply predicting based on 0.5% of patients who have cancer 
          function y = predictCancer(x)
  y = 0;
  return
    • Let’s say you have
      • 99.2% accuracy
        • 0.8% error
      • If you improve your algorithm to become 99.5% accuracy
        • 0.5% error
        • It might be the case of just predicting whether you have cancer that would yield this error
  • Precision/Recall
    • By calculating precision/recall, we will have a better sense of how our algorithm is doing
      • If y = 0
        • Recall = 0
        • This shows that the classifier is not good

2b. Trading off Precision and Recall

  • If we want to avoid false positives
    • We want to be more confident before predicting cancer (y = 1)
    • We can increase the threshold of h0(x) from 0.5 to 0.7 or even 0.9
    • Result
      • False positives: decrease
      • True positives: decrease
      • Recall: decrease
      • Precision: higher
  • If we want to avoid false negatives
    • We want to avoid missing too many cases of cancer
    • We can decrease the threshold of h0(x) from 0.5 to 0.3
    • Result
      • False negatives: decrease
      • True positive: increase
      • Recall: higher
      • Precision: lower
  • Many different precision recall curve, but here is one example
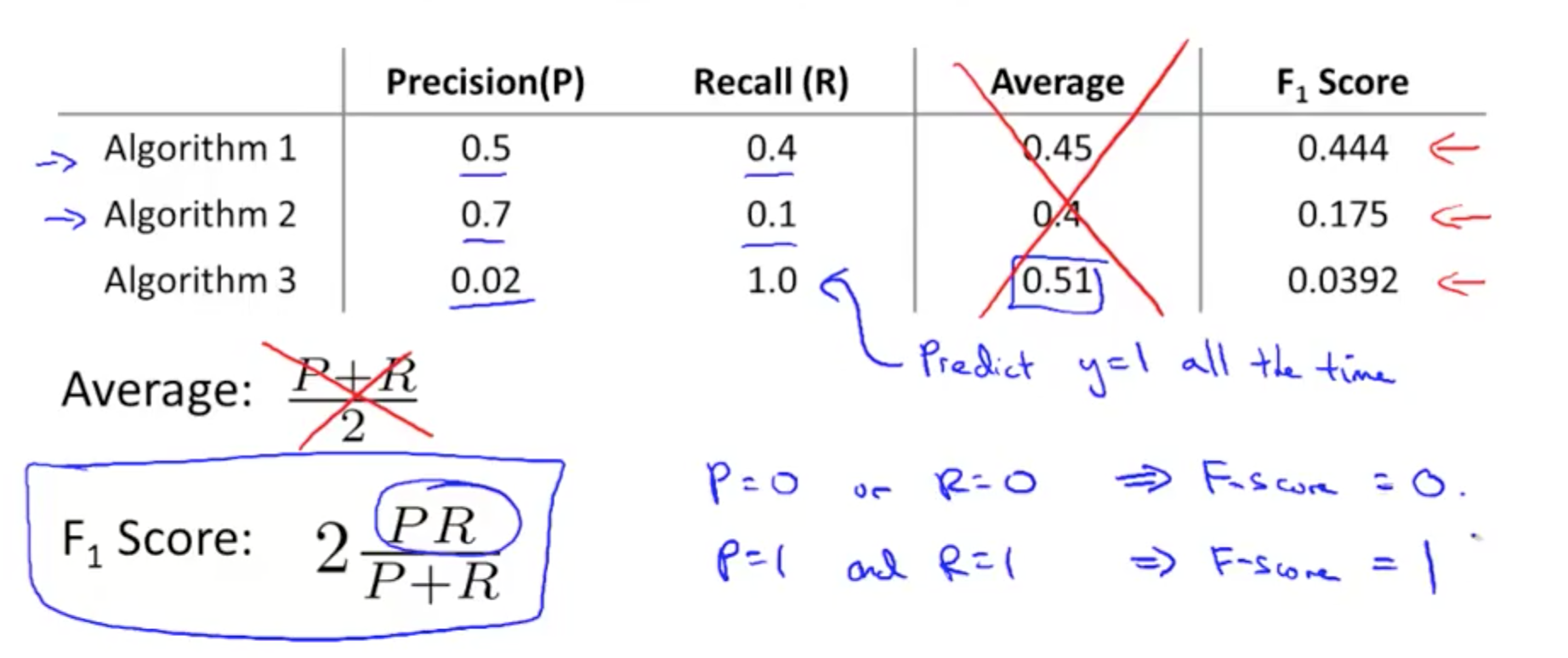
  • How do we compare precision/recall numbers? Which pair is best?
    • We can use an average
      • At the extremes, neither classifiers is good
      • If we predict y = 1 all the time, it’s a useless classifier even though if it has a high recall
      • But average is not good because the extreme scenarios may have a lower average than other combinations that may be better
    • We should use the F score (F1 score)
      • F1 Score = (2 * P * R) / (P + R)
      • Remember to measure P and R on the cross-validation set and choose the threshold which maximizes the F-score

3. Using Large Data Sets

  • Under certain conditions, getting a lot of data and training a learning algorithm would result in very good performance
  • Designing a high accuracy learning system
    • Classify between confusable words
      • to, two, too
      • then, than
    • For breakfast, I ate two eggs
    • Algorithms
      • Perceptron (logistic regression)
      • Winnow (less popular)
      • Memory-based (less popular)
      • Naive Bayes (popular)
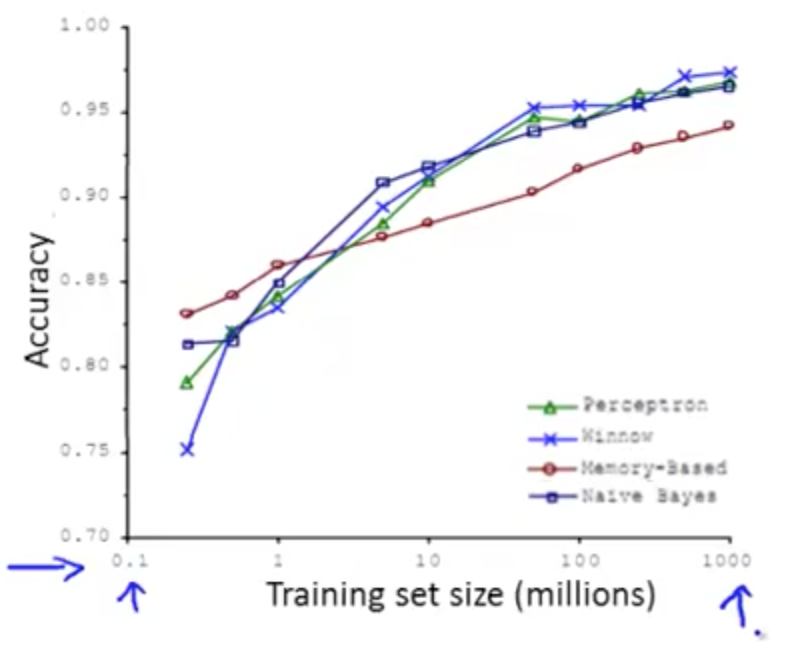
    • Algorithms give roughly similar performance
      • With larger training set, all algorithms’ precision increase
  • Often, it is not who has the best algorithm, but who has the most data
  • Large data rationale
  • In sum
    • Low bias: use complex algorithm
    • Low variance: use large training set
Tags: machine_learning