Naive Bayes Methods¶

Bayes Rule: Intuitive Explanation

(Prior probability)(Test evidence) --> (Posterior probability)
Example
- P(C) = 0.01
- 90% it is positive if you have C (Sensitivity)
- 90% it is negative if you don't have C (Specificity)
  - prior
    - P(C) = 0.01
    - P(C') = 0.99
    - P(Pos|C) = 0.9
      - P(Pos|C') = 0.1
    - P(Neg|C') = 0.9
      - P(Neg|C) = 0.1
  - joint
    - P(C and Pos) = P(C)P(Pos|C) = (0.01)(0.9) = 0.009
    - P(C'and Pos) = P(C')P(Pos|C') = (0.99)(0.1) = 0.099
  - normalizer
    - P(Pos) = P(C and Pos) + P(C' and Pos) = 0.108
  - posterior
    - P(C|Pos) = 0.009 / 0.108 = 0.0833
    - P(C'|Pos) = 0.099 / 0.108 = 0.9167
      - Adding both = 1.0

Bayes Rule: Example

This is really good for text learning
Example
- P(Chris) = 0.5
  - P(Love|Chris) = 0.1
  - P(Deal|Chris) = 0.8
  - P(Life|Chris) = 0.1
- P(Sara) = 0.5
  - P(Love|Sara) = 0.5
  - P(Love|Deal) = 0.2
  - P(Love|Life) = 0.3

p_chris_and_love_deal = 0.1*0.8*0.5

p_sara_and_love_deal = 0.5*0.2*0.5

normalizer = p_chris_and_love_deal + p_sara_and_love_deal

p_chris_given_love_deal = p_chris_and_love_deal / normalizer
p_sara_given_love_deal = p_sara_and_love_deal / normalizer

# P(Chris | "Love Deal")
print(p_chris_given_love_deal)

# P(Sara | "Love Deal")
print(p_sara_given_love_deal)

0.4444444444444445
0.5555555555555555

Bayes Rule: Theory

Learn the best hypothesis given data and some domain knowledge
- Learn the most probable hypothesis given data and domain knowledge
- $$\underset{h∈H}{\mathrm{argmax}}P(h|D)$$
  - h: some hypothesis
  - D: some data
  - argmax h∈H
    - We want to maximize P(h|D)
Bayes rule
- $$P(h|D) = \frac{P(D|h)P(h)}{P(D)}$$
  - $$P(a,b) = P(a|b)P(b)$$
  - $$P(a,b) = P(b|a)P(a)$$
    - P(a,b) is the probability of a and b
  - P(D)
    - This is a normalizing term
    - Prior on the data
  - P(D|h)
    - Data given the hypothesis
    - $$D =\{x_i, d_i\}$$
    - Training data, D, with inputs (x) and labels (d)
    - What's the likelihood that given all of x_i and P(D|h) hypothesis is true, we will observe d's
  - P(h)
    - Prior on h
    - Domain knowledge
      - Say if you use KNN, you believe points close together would give similar outputs with higher likelihood than those far from one another

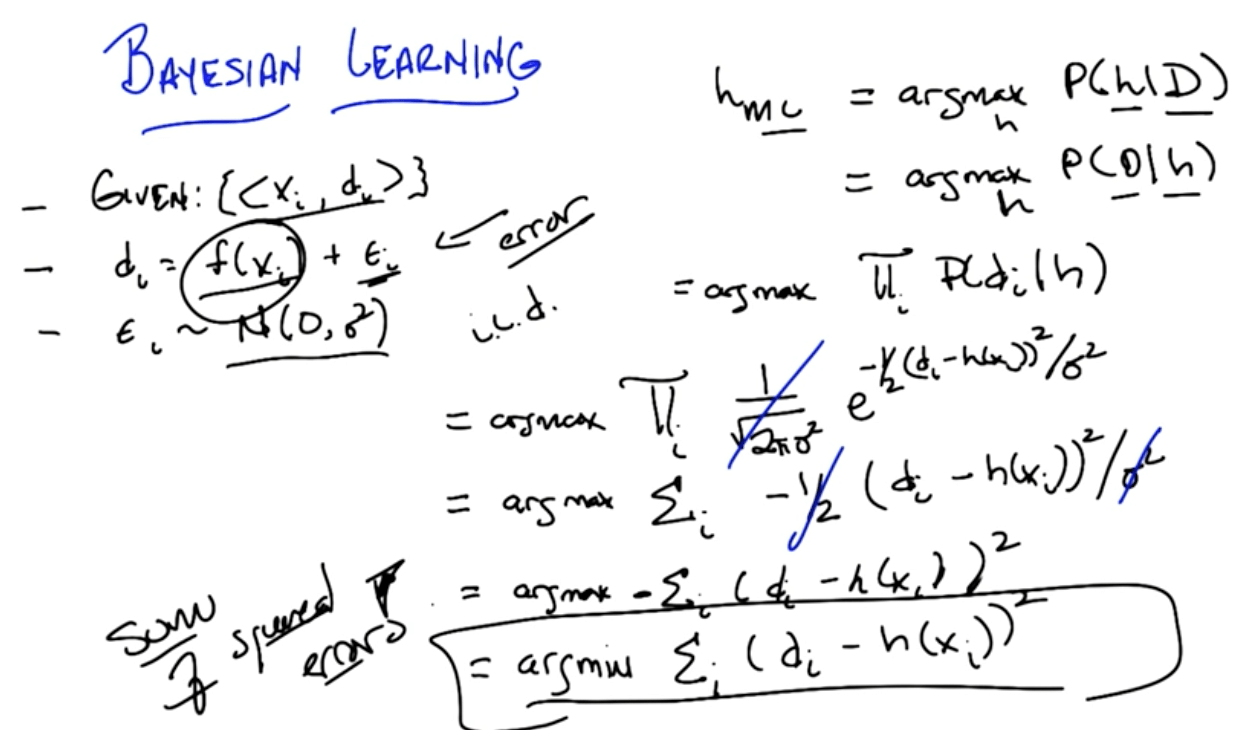
Bayesian Learning Algorithm

For each h∈H, calculate P(h|D) ≈ P(D|h)
- Output
  - $$h_1 = \underset{h}{\mathrm{argmax}}P(h|D)$$
    - h_1: Maximum a posteriori
  - $$h_2 = \underset{h}{\mathrm{argmax}}P(D|h)$$
    - h_2: Maximum likelihood
    - We're assuming P(h) and P(D) are uniform
      - They're constants so we can ignore

Gaussian Naive Bayes

Ultimately we've simplified, using Gaussian distribution, to minimizing the sum of squared errors!
Based on bayes rule we've ended up deriving sum of squared error

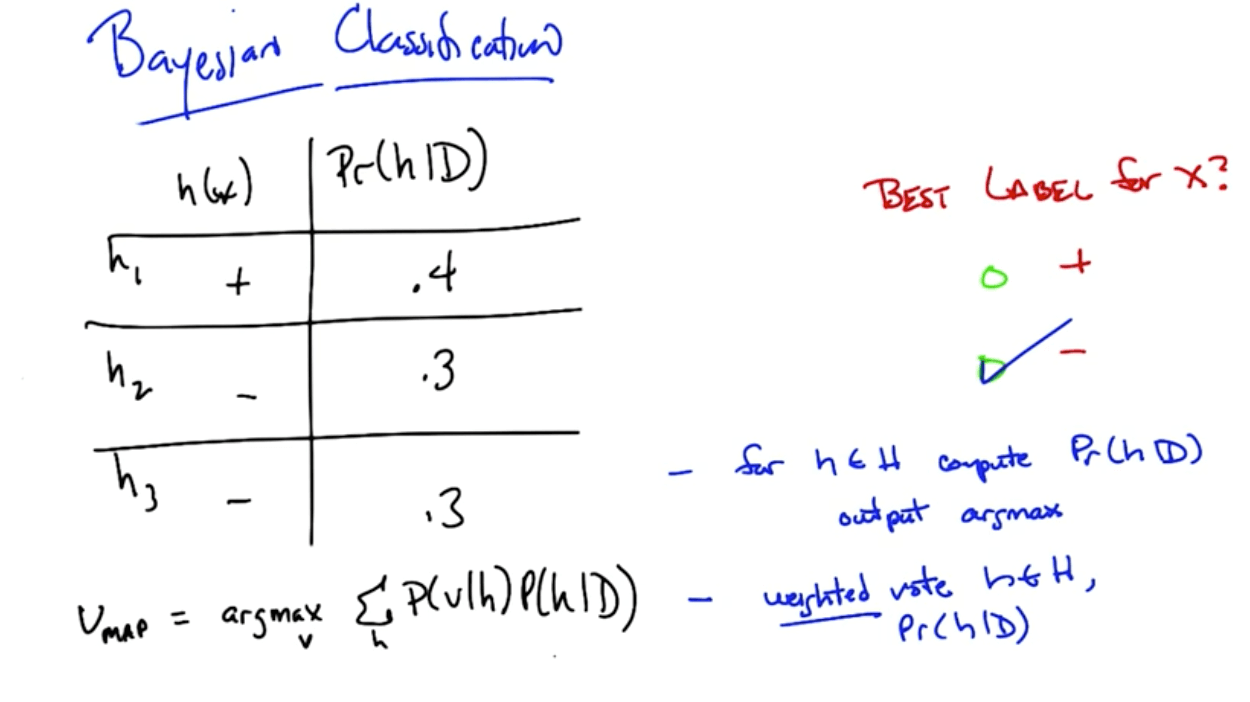
Bayesian Classification

The algorithm changes slightly here
- We are maximizing the weighted vote instead of simply P(h|D)

Version Space

The version space is a subset of the hypothesis space, where the hypotehesis space is a space of all possible hypotheses
The version space are those hypotheses such that they correctly predict the training data you have (essentially a 100% model fit)

Bayesian Networks, Bayesian Nets, Belief Networks or Graphical Models

Representing and dealing with probabilities
Conditional independence
- X is conditionally independent of Y given Z if the probability distribution governing X is independent of the value of y given the value of Z
  - P(X=x | Y=y, Z=z) = P(X=x | Z=z)
  - More compactly
    - P(X|Y,Z) = P(X|Z)
Order of graph must be topological
- Graph must be acylic
  - No cycles
Sampling
- Two things distributions are for
  - Probability of value
  - Generate values
- Reasons for sampling
  - Simulation of a complex process
  - Approximate inference
    - For machines
    - We can't find the exact values because it may be hard and slower
  - Visualization
    - For humans to get a feel
Inferencing Rules
- Marginalization
  - $$P(x) = \underset{y}\sum(x,y)$$
- Chain rule
  - $$P(x,y) = P(y|x)P(x) = P(y|x)P(y)$$
- Bayes rule
  - $$P(y|x) = \frac {P(x|y)P(y)}{P(x)}$$

Naive Bayes

Say you've label A and B (hidden)
- Label A
  - Have multiple words with different probabilities
  - Every word gives evidence if it's label A
  - We mutiply all the probabilities with the prior to find the joint probability of A
- Label B
  - Have multiple words with different probabilities
  - Every word gives evidence if it's label B
  - We multiply all the probabilities with the prior to find the joint probability of B
- Now you can find out the probability of it being A or B
Reason why it's called Naive
- It ignores word order!

Naive Bayes Benefits

Inference is cheap
- Linear
Few parameters
Estimate parameters with labeled data
Connects inference and classification
Empirically successful

Naive Bayes Training

In the training process of a Bayes calssification problem, the sample data does the following:
1. Estimate likelihood distributions of X for each value of Y
2. Estimate prior probability P(Y=j)

Gaussian Naive Bayes in Scikit-learn

from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score

# Create features' DataFrame and response Series
iris = load_iris()
X = iris.data
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=6)

# Instantiate: create object
gnb = GaussianNB()

# Fit
gnb.fit(X_train, y_train)

# Predict
y_pred = gnb.predict(X_test)

# Accuracy
acc = accuracy_score(y_test, y_pred)
acc

0.92105263157894735