Decision Trees, ID3, Entropy, Information again and more.
Decision Trees with Scikit-learn

Decision Trees Classification Model

  • Supervised Learning
  • Classification
    • Taking an input X
    • Mapping to a discrete label y

Classification learning terms

  • Instances
    • Input
      • Pictures
      • Credit score examples
  • Concept
    • Function (mappings from objects to members of a set)
      • Takes input and maps the input to an output
  • Target concept
    • The answer we want
    • The function we want
  • Hypothesis Class
    • Set of all concepts you're willing to entertain
    • All functions we care about (classification-only)
  • Sample
    • Training set
  • Candidate
    • Concept that you think might be the target concept
    • Concept = Target Concept
  • Testing set
    • Take candidate concept and test if it does a good job

Decision Trees Introduction

  • It's simply asking a series of questions
  • You'll have decision nodes
    • Pick an attribute and ask a question (is sex male?)
      • Values = edges (lines)
        • Yes
          • Ask a different question (sub-node)
        • No
          • Ask a different question (sub-node)
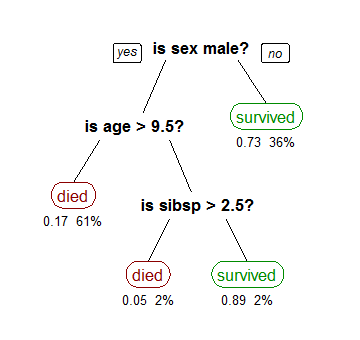
  • Decision Tree
    • As you can see here, you can continue to ask more questions with more nodes down the tree.
      • This is an example tree from the Titanic Survivors
  • Intuition
    • Features' headers = questions
      • sex_male
      • age_>_9.5
      • sibsp_>_2.5
    • Features = answers

Decision Trees: Learning

  1. Pick best attribute
  2. Ask question
  3. Follow the answer path
  4. Go to (1)
    • Repeat until you get an answer

Decision Trees: Expressiveness

  • n-OR: ANY
    • You need n number (linear) of nodes
      • Easy!
  • n-XOR: ODD PARITY
    • If the number of attributes that are true = odd, output of the function would be true
      • Otherwise, false
    • You need 2^N number (exponential) of nodes
      • Hard!

ID3 Algorithm

  • A: best attribute
  • Assign A as decision attribute for node
  • For each value of A, create a descendant of node
  • Sort training examples to leaves
  • If examples perfectly classified, stop
    • Else, iterate over leaves

ID3: Bias

  • Restriction Bias
    • Restricted to hypothesis
    • Example: only those considered in a decision tree
  • Preference Bias
    • What sort of hypothesis we prefer
  • Inductive bias
    • ID3 would prefer tree that has good splits near the top
      • Prefers correct over incorrect
      • Prefers shorter trees

Choosing Best Attributes: Information Gain

  • Goal is to minimize entropy for maximum information gain
  • Formula
  • If all samples went to left side of tree
    • No entropy gain in using that attribute
    • Entropy constant
  • If all samples went to each side of the tree with no clear split (all mixed up)
    • No entropy gain
    • Entropy constant
  • If samples split into each side of the tree distinctly
    • Max entropy gain
    • Entropy fell

Decision Trees: Other Considerations

  • What happens if we have continuous attributes?
    • Age, weight, distance, etc.
    • Create attribute with a range
      • 20 <= age < 30
      • This would return True or False
  • You can repeat an attribute along a path for continuous attributes
    • Ask 20 <= age < 30
    • Ask age > 30 etc.
    • But it does not make sense to repeat an attribute for discrete attributes!
  • When do we stop?
    • No overfitting (when the tree gets too big)!
      • Solution? Pruning
        • Hold out a validation set
        • To build a full tree
        • Cut leaves then check against validation set
        • If error is low enough, stop expanding the tree

Scikit-learn for Decision Trees

In [1]:
# Import
from sklearn.tree import DecisionTreeClassifier
from sklearn.cross_validation import train_test_split
In [2]:
# Load iris dataset
from sklearn.datasets import load_iris

# Instantiate
iris = load_iris()

# Create training and feature
X = iris.data
y = iris.target

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
In [24]:
# Same 3-step process

# 1. Instantiate
# default criterion=gini
# you can swap to criterion=entropy 
dtc = DecisionTreeClassifier(random_state=0)

# 2. Fit
dtc.fit(X_train, y_train)

# 3. Predict, there're 4 features in the iris dataset
y_pred_class = dtc.predict(X_test)

Evaluating with Accuracy

In [4]:
from sklearn import metrics
In [5]:
# Accuracy
metrics.accuracy_score(y_test, y_pred_class)
Out[5]:
0.97368421052631582

Dealing with overfitting: min_samples_split

  • default min_samples_split=2
    • This means if you've 1 sample left in a node, you cannot split further
    • When it gets really deep in depth, it overfits your data
  • If you increase your min_samples_split value
    • You would decrease the depth of your tree
    • This is because you would run out of samples to split
    • This would reduce overfitting
In [11]:
# 1. Instantiate with min_samples_split = 50
dtc = DecisionTreeClassifier(min_samples_split=4, random_state=0)

# 2. Fit
dtc.fit(X_train, y_train)

# 3. Predict, there're 4 features in the iris dataset
y_pred_class = dtc.predict(X_test)

# Accuracy
metrics.accuracy_score(y_test, y_pred_class)
Out[11]:
0.97368421052631582

Using GridSearchCV for optimizing parameters

In [9]:
# Import
from sklearn.grid_search import GridSearchCV

# Define the parameter values that should be searched
sample_split_range = list(range(1, 50))

# Create a parameter grid: map the parameter names to the values that should be searched
# Simply a python dictionary
# Key: parameter name
# Value: list of values that should be searched for that parameter
# Single key-value pair for param_grid
param_grid = dict(min_samples_split=sample_split_range)

# instantiate the grid
grid = GridSearchCV(dtc, param_grid, cv=10, scoring='accuracy')

# fit the grid with data
grid.fit(X_train, y_train)
Out[9]:
GridSearchCV(cv=10, error_score='raise',
       estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
            max_features=None, max_leaf_nodes=None, min_samples_leaf=1,
            min_samples_split=42, min_weight_fraction_leaf=0.0,
            presort=False, random_state=0, splitter='best'),
       fit_params={}, iid=True, n_jobs=1,
       param_grid={'min_samples_split': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49]},
       pre_dispatch='2*n_jobs', refit=True, scoring='accuracy', verbose=0)
In [10]:
# examine the best model

# Single best score achieved across all params (min_samples_split)
print(grid.best_score_)

# Dictionary containing the parameters (min_samples_split) used to generate that score
print(grid.best_params_)

# Actual model object fit with those best parameters
# Shows default parameters that we did not specify
print(grid.best_estimator_)

0.973214285714
{'min_samples_split': 4}
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
            max_features=None, max_leaf_nodes=None, min_samples_leaf=1,
            min_samples_split=4, min_weight_fraction_leaf=0.0,
            presort=False, random_state=0, splitter='best')

Entropy

  • Controls how a Decision Tree decides where to split the data
  • Definition
    • Measure of impurity in a bunch of examples
    • Opposite of purity
  • Concept
    • Find variables and split
    • Split such that the sets contain the least impurities
    • Repeat the process until sets are pure
  • Values Entropy can hold values between 0 and 1.0
    • All examples same class
      • Entropy = 0
    • All examples are evenly split amongst classes
      • Entropy = 1.0
  • Formula
      • p(i) is the fraction of examples in class i
      • sum over all classes
  • Example of Formula
    • Assume 2 classes for the node
      • slow (2 examples)
      • fast (2 examples)
    • p(slow) = fraction of slow over all examples = 2/4 = 0.5
    • p(fast) = fraction of fast over all examples = 2/4 = 0.5
    • entropy = -p(slow)log2(pslow) + (-p(fast)log2(pslow))
In [17]:
# Calculating impurity from the example above
# Maximum state of impurity, 1.0
import numpy as np
-0.5*np.log2(0.5) + (-0.5*np.log2(0.5))
Out[17]:
1.0

Information gain

  • Formula
    • information gain = entropy(parent) - [weighted average]entropy(children)
      • weight = number of examples in set / total number of examples
  • Decision tree algorithm: maximizing information gain
  • Example
    • Assume the feature "grade" has the following details
      • Steep (Slow, S)
      • Steep (Slow, S)
      • Flat (Fast, F)
      • Steep (Fast, F)
    • If we split based on "grade": is it steep?
      • Child 1: Flat (Fast)
      • Child 2: Steep (Slow, Slow, Fast)
In [19]:
# Entropy of child 1 = 0
# Perfect split for this child

# Entropy of child 2 = 0.918
-(2/3)*np.log2(2/3) - (1/3)*np.log2(1/3)
Out[19]:
0.91829583405448956
In [22]:
# Weighted average of entropy(children)
(3/4)*(0.9184) + (1/4)*0
Out[22]:
0.6888
In [23]:
# Entropy Gain
1 - (3/4)*(0.9184) + (1/4)*0
Out[23]:
0.31120000000000003

Decision Trees

  • Prone to overfitting
    • If you have a lot of features
    • Stop growth of tree at the appropriate time
  • You can build bigger classifiers out of this
    • It is called ensemble classifiers
Tags: machine_learning