Cross-Validation for Parameter Tuning, Model Selection, and Feature Selection
Cross-Validation for Parameter Tuning, Model Selection, and Feature Selectio

Topics

  1. Review of model evaluation procedures
  2. Steps for K-fold cross-validation
  3. Comparing cross-validation to train/test split
  4. Cross-validation recommendations
  5. Cross-validation example: parameter tuning
  6. Cross-validation example: model selection
  7. Cross-validation example: feature selection
  8. Improvements to cross-validation
  9. Resources

This tutorial is derived from Data School's Machine Learning with scikit-learn tutorial. I added my own notes so anyone, including myself, can refer to this tutorial without watching the videos.

1. Review of model evaluation procedures

Motivation: Need a way to choose between machine learning models

  • Goal is to estimate likely performance of a model on out-of-sample data

Initial idea: Train and test on the same data

  • But, maximizing training accuracy rewards overly complex models which overfit the training data

Alternative idea: Train/test split

  • Split the dataset into two pieces, so that the model can be trained and tested on different data
  • Testing accuracy is a better estimate than training accuracy of out-of-sample performance
  • Problem with train/test split
    • It provides a high variance estimate since changing which observations happen to be in the testing set can significantly change testing accuracy
    • Testing accuracy can change a lot depending on a which observation happen to be in the testing set
In [1]:
from sklearn.datasets import load_iris
from sklearn.cross_validation import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
In [2]:
# read in the iris data
iris = load_iris()

# create X (features) and y (response)
X = iris.data
y = iris.target
In [3]:
# use train/test split with different random_state values
# we can change the random_state values that changes the accuracy scores
# the accuracy changes a lot
# this is why testing accuracy is a high-variance estimate
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=6)

# check classification accuracy of KNN with K=5
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
metrics.accuracy_score(y_test, y_pred)
Out[3]:
0.97368421052631582

Question: What if we created a bunch of train/test splits, calculated the testing accuracy for each, and averaged the results together?

Answer: That's the essense of cross-validation!

2. Steps for K-fold cross-validation

  1. Split the dataset into K equal partitions (or "folds")
    • So if k = 5 and dataset has 150 observations
    • Each of the 5 folds would have 30 observations
  2. Use fold 1 as the testing set and the union of the other folds as the training set
    • Testing set = 30 observations (fold 1)
    • Training set = 120 observations (folds 2-5)
  3. Calculate testing accuracy
  4. Repeat steps 2 and 3 K times, using a different fold as the testing set each time
    • We will repeat the process 5 times
    • 2nd iteration
      • fold 2 would be the testing set
      • union of fold 1, 3, 4, and 5 would be the training set
    • 3rd iteration
      • fold 3 would be the testing set
      • union of fold 1, 2, 4, and 5 would be the training set
    • And so on...
  5. Use the average testing accuracy as the estimate of out-of-sample accuracy

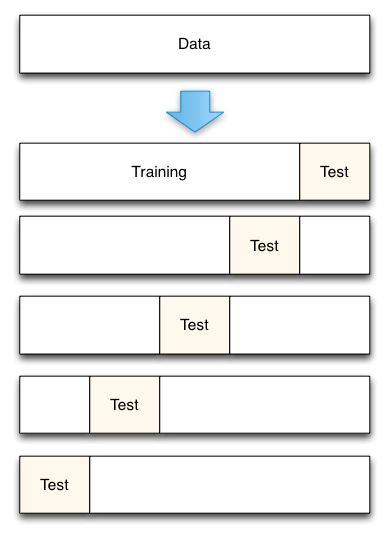
Diagram of 5-fold cross-validation:

5-fold cross-validation

In [4]:
# simulate splitting a dataset of 25 observations into 5 folds
from sklearn.cross_validation import KFold
kf = KFold(25, n_folds=5, shuffle=False)


# print the contents of each training and testing set
# ^ - forces the field to be centered within the available space
# .format() - formats the string similar to %s or %n
# enumerate(sequence, start=0) - returns an enumerate object
print('{} {:^61} {}'.format('Iteration', 'Training set obsevations', 'Testing set observations'))
for iteration, data in enumerate(kf, start=1):
    print('{!s:^9} {} {!s:^25}'.format(iteration, data[0], data[1]))

Iteration                   Training set obsevations                    Testing set observations
    1     [ 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]        [0 1 2 3 4]
    2     [ 0  1  2  3  4 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]        [5 6 7 8 9]
    3     [ 0  1  2  3  4  5  6  7  8  9 15 16 17 18 19 20 21 22 23 24]     [10 11 12 13 14]
    4     [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 20 21 22 23 24]     [15 16 17 18 19]
    5     [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19]     [20 21 22 23 24]
  • Dataset contains 25 observations (numbered 0 through 24)
  • 5-fold cross-validation, thus it runs for 5 iterations
  • For each iteration, every observation is either in the training set or the testing set, but not both
  • Every observation is in the testing set exactly once

3. Comparing cross-validation to train/test split

Advantages of cross-validation:

  • More accurate estimate of out-of-sample accuracy
  • More "efficient" use of data
    • This is because every observation is used for both training and testing

Advantages of train/test split:

  • Runs K times faster than K-fold cross-validation
    • This is because K-fold cross-validation repeats the train/test split K-times
  • Simpler to examine the detailed results of the testing process

4. Cross-validation recommendations

  1. K can be any number, but K=10 is generally recommended
    • This has been shown experimentally to produce the best out-of-sample estimate
  2. For classification problems, stratified sampling is recommended for creating the folds
    • Each response class should be represented with equal proportions in each of the K folds
      • If dataset has 2 response classes
        • Spam/Ham
        • 20% observation = ham
        • Each cross-validation fold should consist of exactly 20% ham
    • scikit-learn's cross_val_score function does this by default

5. Cross-validation example: parameter tuning

Goal: Select the best tuning parameters (aka "hyperparameters") for KNN on the iris dataset

  • We want to choose the best tuning parameters that best generalize the data
In [5]:
from sklearn.cross_validation import cross_val_score
In [6]:
# 10-fold cross-validation with K=5 for KNN (the n_neighbors parameter)
# k = 5 for KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)

# Use cross_val_score function
# We are passing the entirety of X and y, not X_train or y_train, it takes care of splitting the dat
# cv=10 for 10 folds
# scoring='accuracy' for evaluation metric - althought they are many
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
print(scores)

[ 1.          0.93333333  1.          1.          0.86666667  0.93333333
  0.93333333  1.          1.          1.        ]
  • In the first iteration, the accuracy is 100%
  • Second iteration, the accuracy is 93% and so on

cross_val_score executes the first 4 steps of k-fold cross-validation steps which I have broken down to 7 steps here in detail

  1. Split the dataset (X and y) into K=10 equal partitions (or "folds")
  2. Train the KNN model on union of folds 2 to 10 (training set)
  3. Test the model on fold 1 (testing set) and calculate testing accuracy
  4. Train the KNN model on union of fold 1 and fold 3 to 10 (training set)
  5. Test the model on fold 2 (testing set) and calculate testing accuracy
  6. It will do this on 8 more times
  7. When finished, it will return the 10 testing accuracy scores as a numpy array
In [7]:
# use average accuracy as an estimate of out-of-sample accuracy
# numpy array has a method mean()
print(scores.mean())

0.966666666667

Our goal here is to find the optimal value of K

In [8]:
# search for an optimal value of K for KNN

# range of k we want to try
k_range = range(1, 31)
# empty list to store scores
k_scores = []

# 1. we will loop through reasonable values of k
for k in k_range:
    # 2. run KNeighborsClassifier with k neighbours
    knn = KNeighborsClassifier(n_neighbors=k)
    # 3. obtain cross_val_score for KNeighborsClassifier with k neighbours
    scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
    # 4. append mean of scores for k neighbors to k_scores list
    k_scores.append(scores.mean())


print(k_scores)

[0.95999999999999996, 0.95333333333333337, 0.96666666666666656, 0.96666666666666656, 0.96666666666666679, 0.96666666666666679, 0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 0.98000000000000009, 0.97333333333333338, 0.97333333333333338, 0.97333333333333338, 0.97333333333333338, 0.98000000000000009, 0.97333333333333338, 0.98000000000000009, 0.96666666666666656, 0.96666666666666656, 0.97333333333333338, 0.95999999999999996, 0.96666666666666656, 0.95999999999999996, 0.96666666666666656, 0.95333333333333337, 0.95333333333333337, 0.95333333333333337]
In [9]:
# in essence, this is basically running the k-fold cross-validation method 30 times because we want to run through K values from 1 to 30
# we should have 30 scores here
print('Length of list', len(k_scores))
print('Max of list', max(k_scores))

Length of list 30
Max of list 0.98
In [10]:
# plot how accuracy changes as we vary k
import matplotlib.pyplot as plt
%matplotlib inline

# plot the value of K for KNN (x-axis) versus the cross-validated accuracy (y-axis)
# plt.plot(x_axis, y_axis)
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-validated accuracy')
Out[10]:
<matplotlib.text.Text at 0x111cb07b8>

The maximum cv accuracy occurs from k=13 to k=20

  • The general shape of the curve is an upside down yield

    • This is quite typical when examining the model complexity and accuracy
    • This is an example of bias-variance trade off
      • Low values of k (low bias, high variance)
        • The 1-Nearest Neighbor classifier is the most complex nearest neighbor model
        • It has the most jagged decision boundary, and is most likely to overfit
      • High values of k (high bias, low variance)
        • underfit
      • Best value is the middle of k (most likely to generalize out-of-sample data)
        • just right

  • The best value of k

    • Higher values of k produce less complex model
      • So we will choose 20 as our best KNN model

6. Cross-validation example: model selection

Goal: Compare the best KNN model with logistic regression on the iris dataset

In [11]:
# 10-fold cross-validation with the best KNN model
knn = KNeighborsClassifier(n_neighbors=20)

# Instead of saving 10 scores in object named score and calculating mean
# We're just calculating the mean directly on the results
print(cross_val_score(knn, X, y, cv=10, scoring='accuracy').mean())

0.98
In [12]:
# 10-fold cross-validation with logistic regression
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
print(cross_val_score(logreg, X, y, cv=10, scoring='accuracy').mean())

0.953333333333

We can conclude that KNN is likely a better choice than logistic regression

7. Cross-validation example: feature selection

Goal: Select whether the Newspaper feature should be included in the linear regression model on the advertising dataset

In [13]:
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
In [14]:
# read in the advertising dataset
data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
In [15]:
# create a Python list of three feature names
feature_cols = ['TV', 'Radio', 'Newspaper']

# use the list to select a subset of the DataFrame (X)
X = data[feature_cols]

# select the Sales column as the response (y)
# since we're selecting only one column, we can select the attribute using .attribute
y = data.Sales
In [16]:
# 10-fold cross-validation with all three features
# instantiate model
lm = LinearRegression()

# store scores in scores object
# we can't use accuracy as our evaluation metric since that's only relevant for classification problems
# RMSE is not directly available so we will use MSE
scores = cross_val_score(lm, X, y, cv=10, scoring='mean_squared_error')
print(scores)

[-3.56038438 -3.29767522 -2.08943356 -2.82474283 -1.3027754  -1.74163618
 -8.17338214 -2.11409746 -3.04273109 -2.45281793]

MSE should be positive

  • But why is the MSE here negative?
  • MSE is a loss function
    • It is something we want to minimize
    • A design decision was made so that the results are made negative
    • The best results would be the largest number (the least negative) so we can still maximize similar to classification accuracy
  • Classification Accuracy is a reward function
    • It is something we want to maximize
In [17]:
# fix the sign of MSE scores
mse_scores = -scores
print(mse_scores)

[ 3.56038438  3.29767522  2.08943356  2.82474283  1.3027754   1.74163618
  8.17338214  2.11409746  3.04273109  2.45281793]
In [18]:
# convert from MSE to RMSE
rmse_scores = np.sqrt(mse_scores)
print(rmse_scores)

[ 1.88689808  1.81595022  1.44548731  1.68069713  1.14139187  1.31971064
  2.85891276  1.45399362  1.7443426   1.56614748]
In [19]:
# calculate the average RMSE
print(rmse_scores.mean())

1.69135317081
In [20]:
# 10-fold cross-validation with two features (excluding Newspaper)
feature_cols = ['TV', 'Radio']
X = data[feature_cols]
print(np.sqrt(-cross_val_score(lm, X, y, cv=10, scoring='mean_squared_error')).mean())

1.67967484191

Without Newspaper

  • Average RMSE = 1.68
  • lower number than with model with Newspaper
    • RMSE is something we want to minimize
    • So the model excluding Newspaper is a better model

8. Improvements to cross-validation

Repeated cross-validation

  • Repeat cross-validation multiple times (with different random splits of the data) and average the results
  • More reliable estimate of out-of-sample performance by reducing the variance associated with a single trial of cross-validation

Creating a hold-out set

  • "Hold out" a portion of the data before beginning the model building process
  • Locate the best model using cross-validation on the remaining data, and test it using the hold-out set
  • More reliable estimate of out-of-sample performance since hold-out set is truly out-of-sample

Feature engineering and selection within cross-validation iterations

  • Normally, feature engineering and selection occurs before cross-validation
  • Instead, perform all feature engineering and selection within each cross-validation iteration
  • More reliable estimate of out-of-sample performance since it better mimics the application of the model to out-of-sample data

9. Resources

Tags: machine_learning