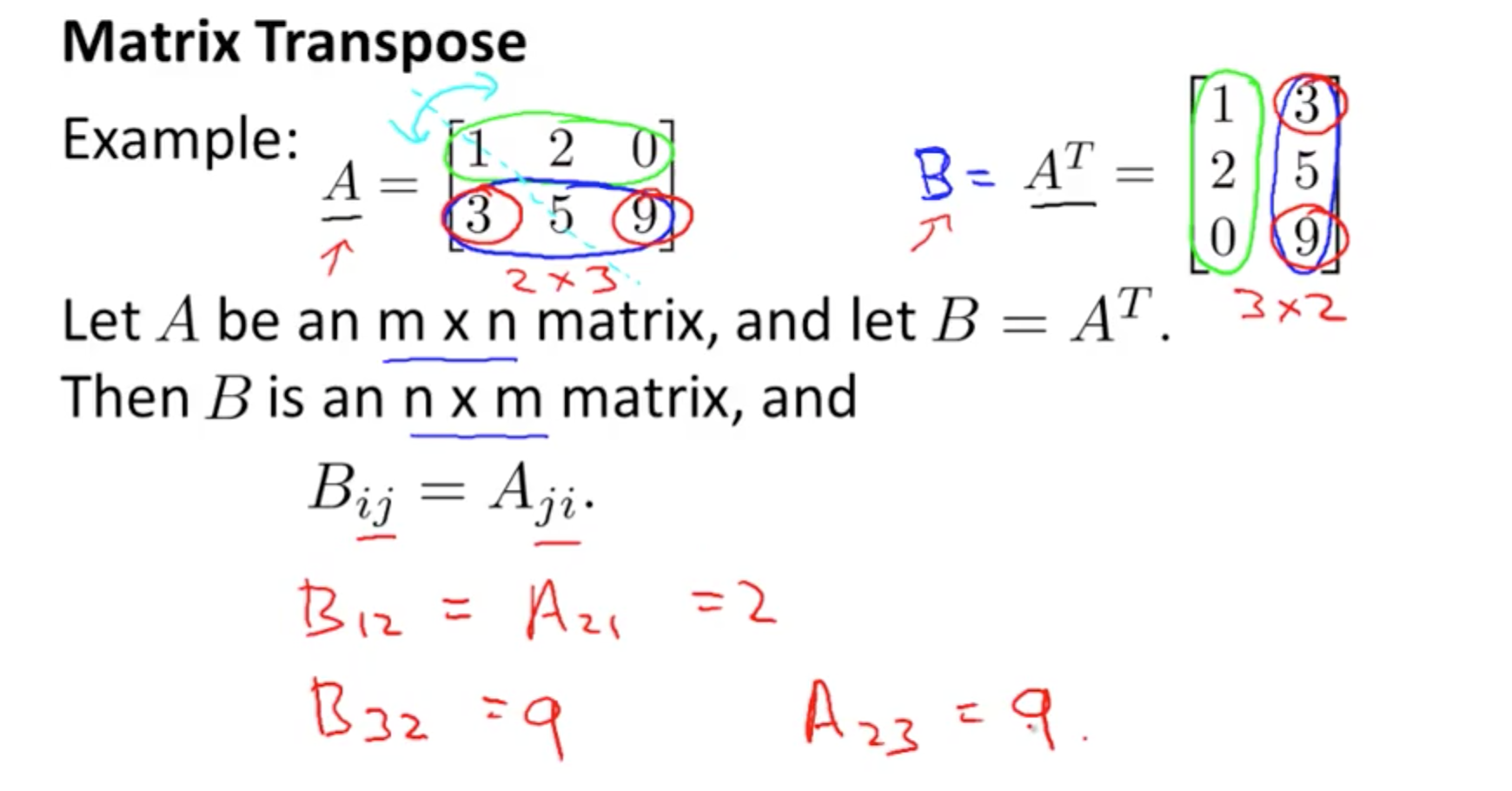Matrices, vectors, addition, scalar multiplication, matrix vector multiplication, matrix matrix multiplication, properties of matrix multiplication, inverse matrix and transposing matrices.

1. Matrices and Vectors

I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.

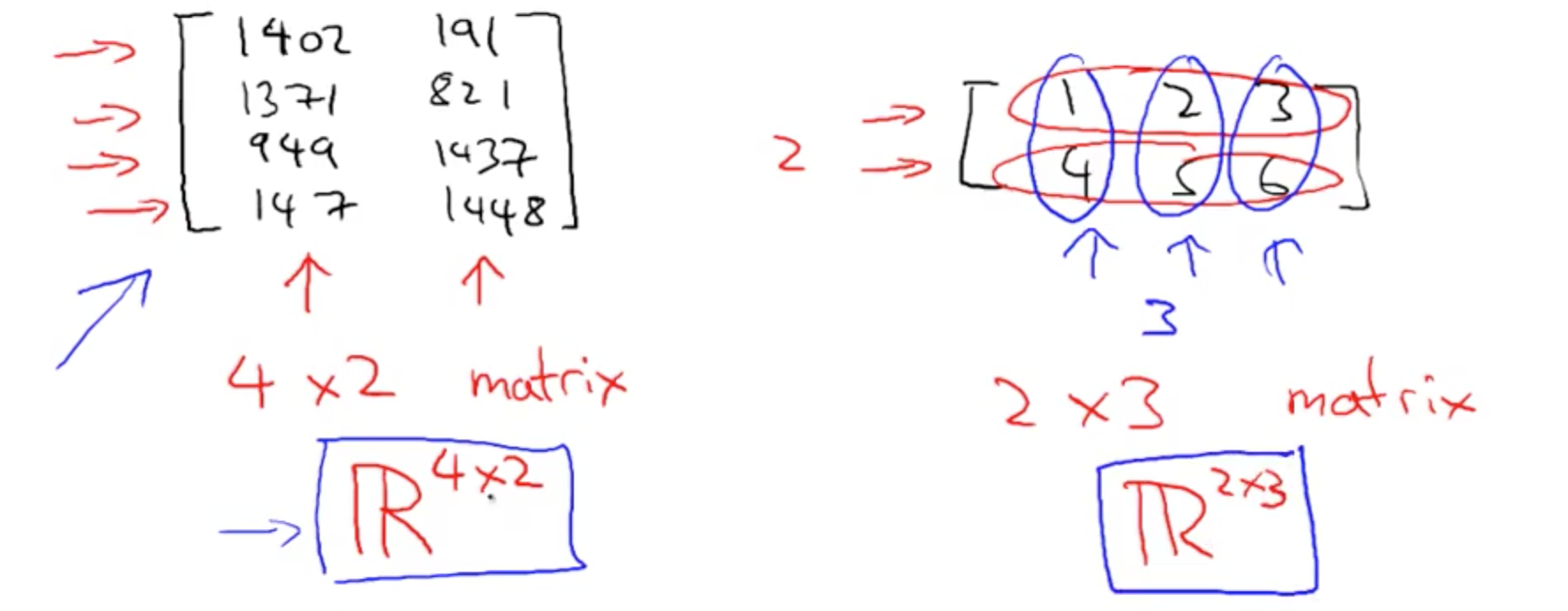
1a. Matrices

  • Rectangular array of numbers
  • 2D array
  • Number of Rows x Number of Columns alt text

1b. Vector

  • n x 1 matrix
  • y(i): i-th element
  • 1-indexed (start from 1-th)
    • Normally this
  • 0-indexed (start from 0-th)
    • Used in Machine Learning

2. Addition and Scalar Multiplication

2a. Addition

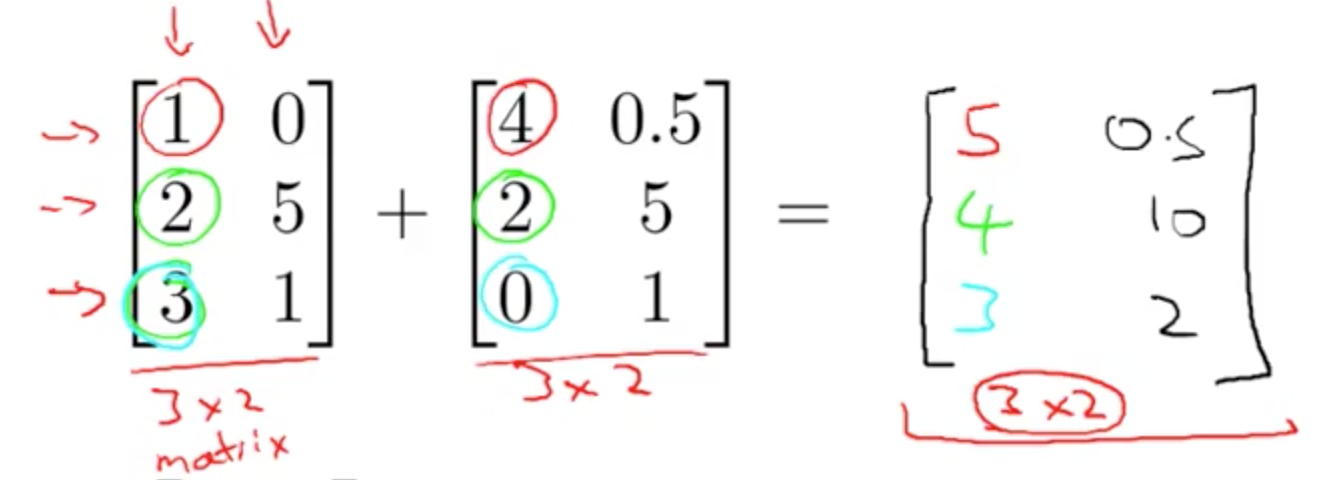
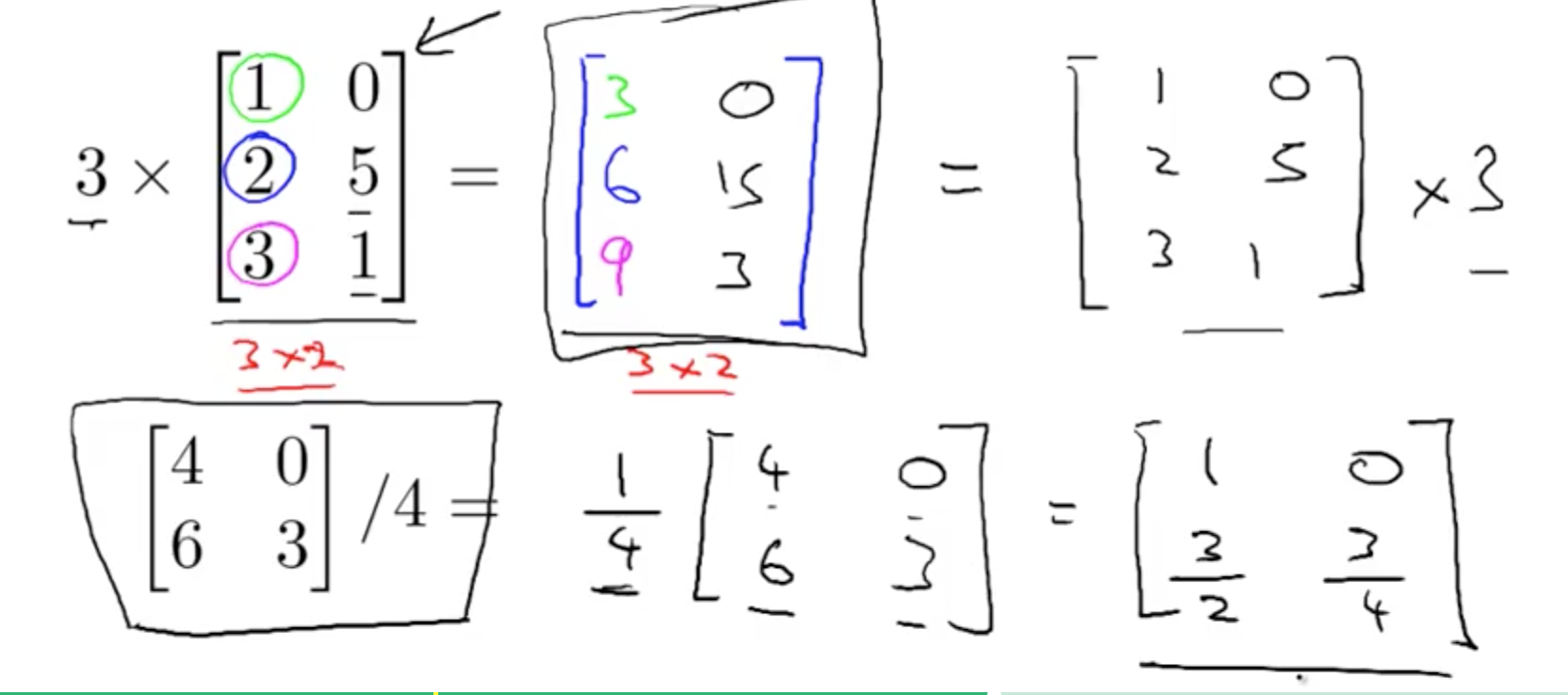
  • You can only add matrices with the same dimensions (r x c) alt text

2b. Scalar (Number) Multiplication

  • Example alt text

3. Matrix Vector Multiplication

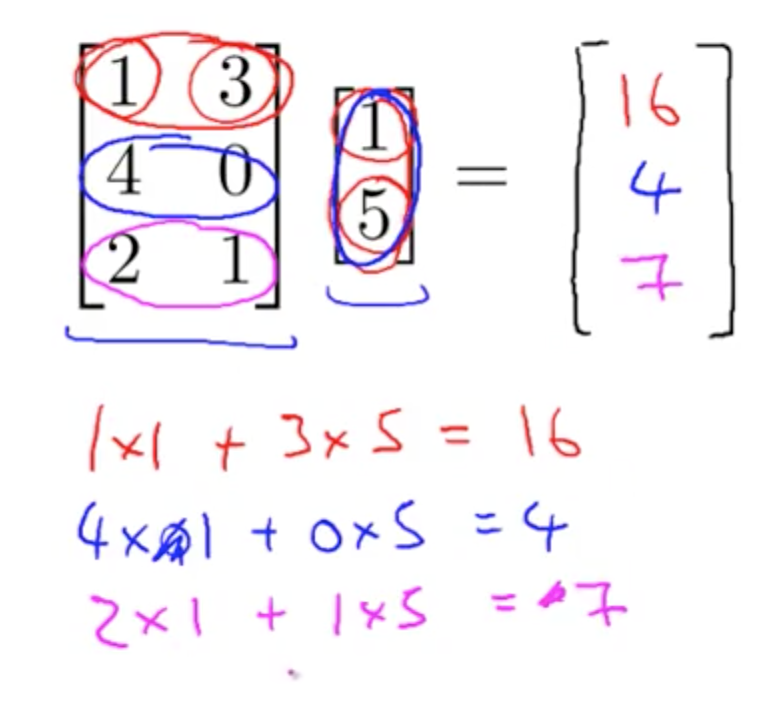
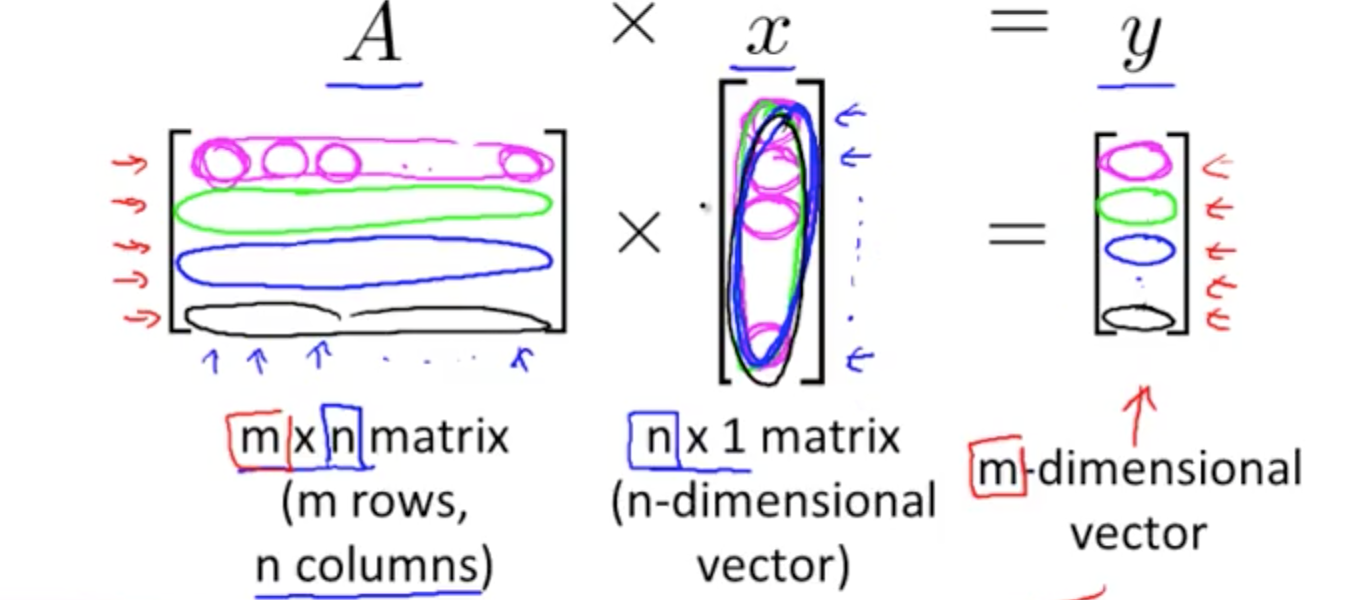
  • Example alt text
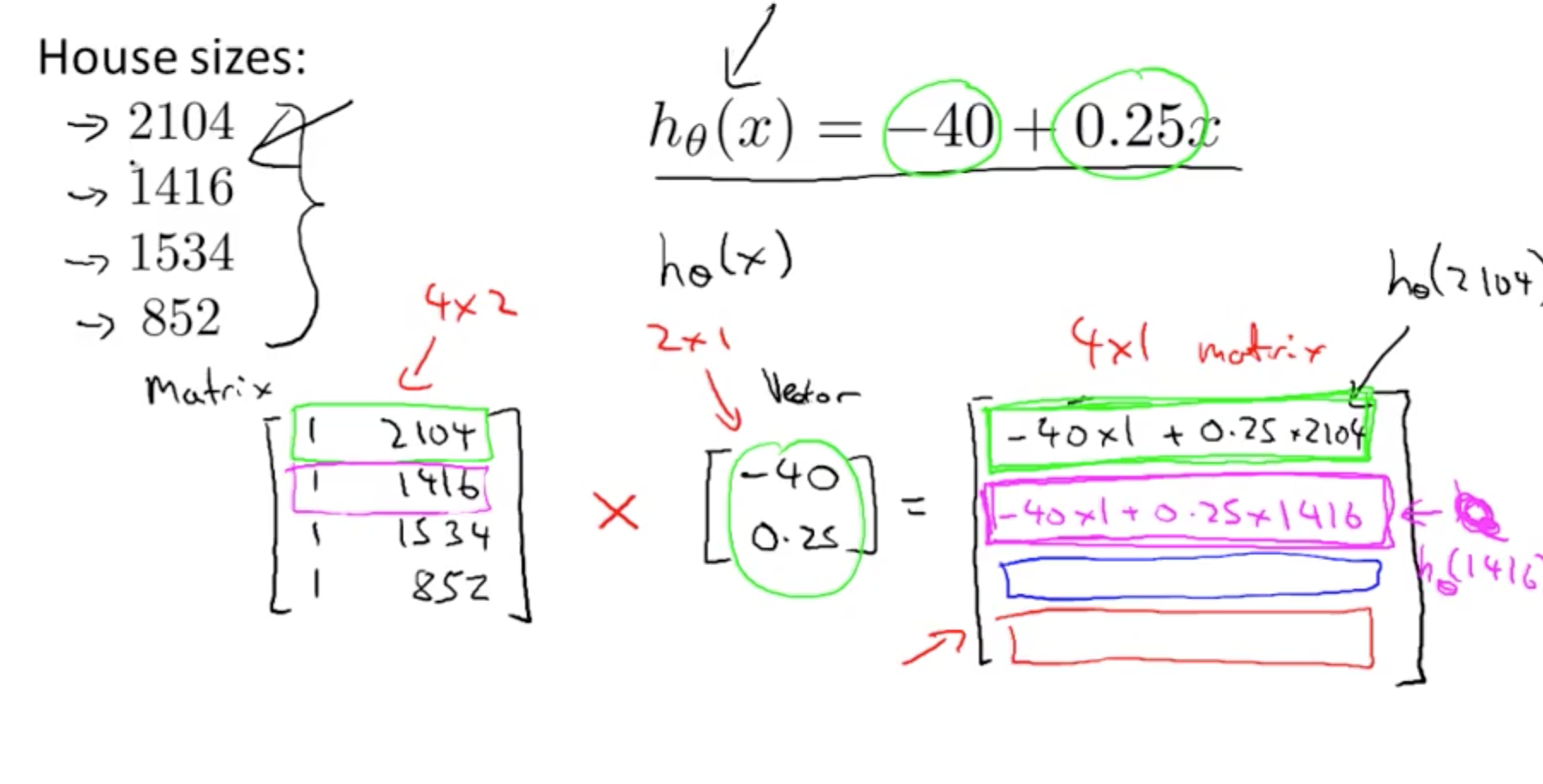
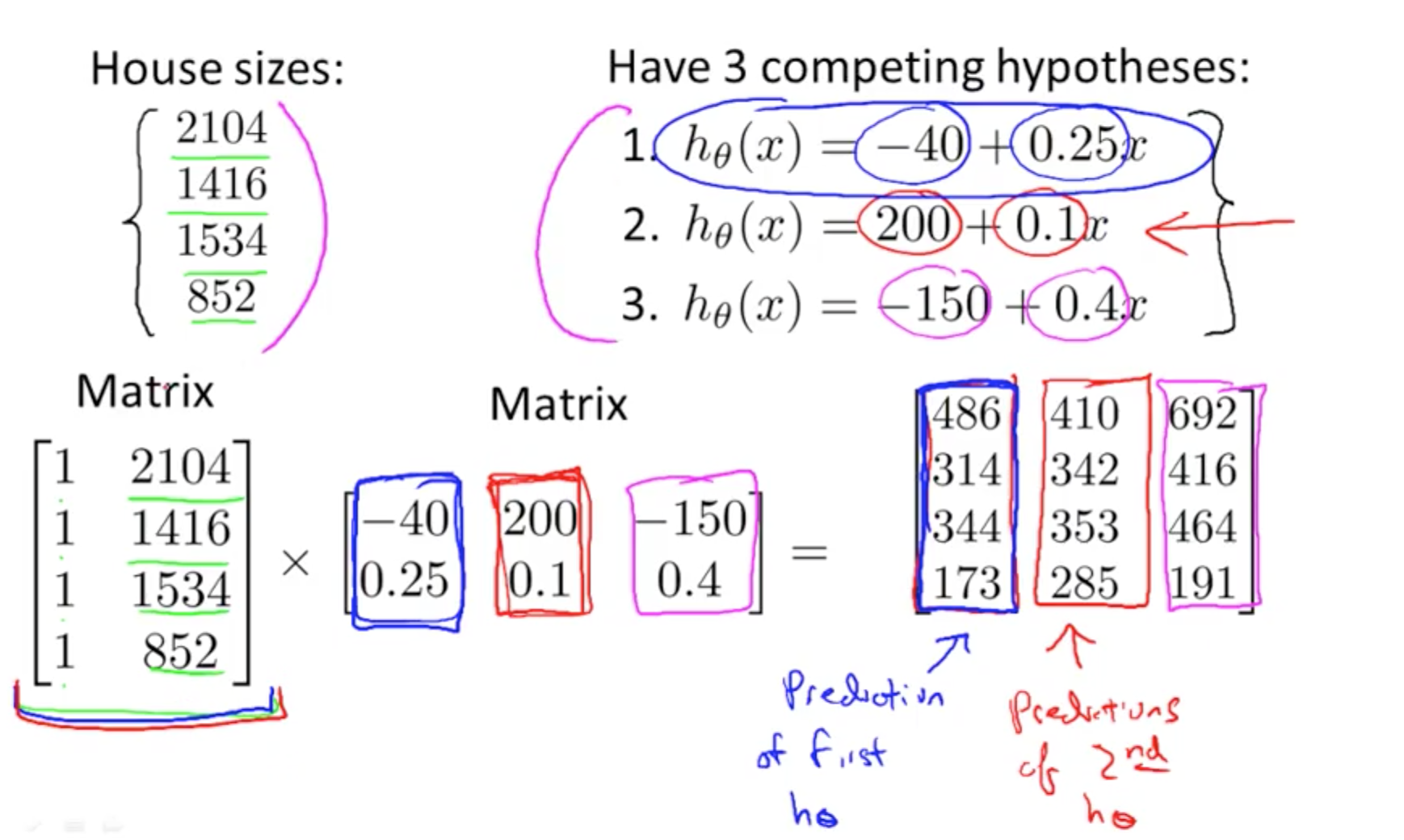
  • Theory alt text
  • Application to hypothesis by converting given data to matrix
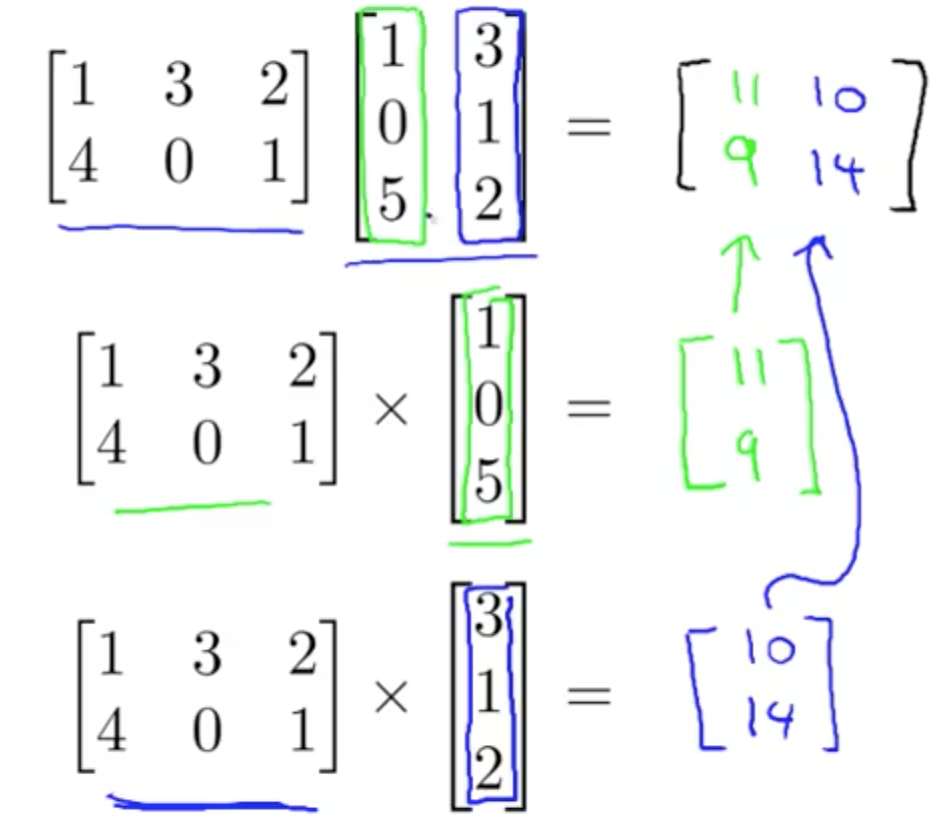
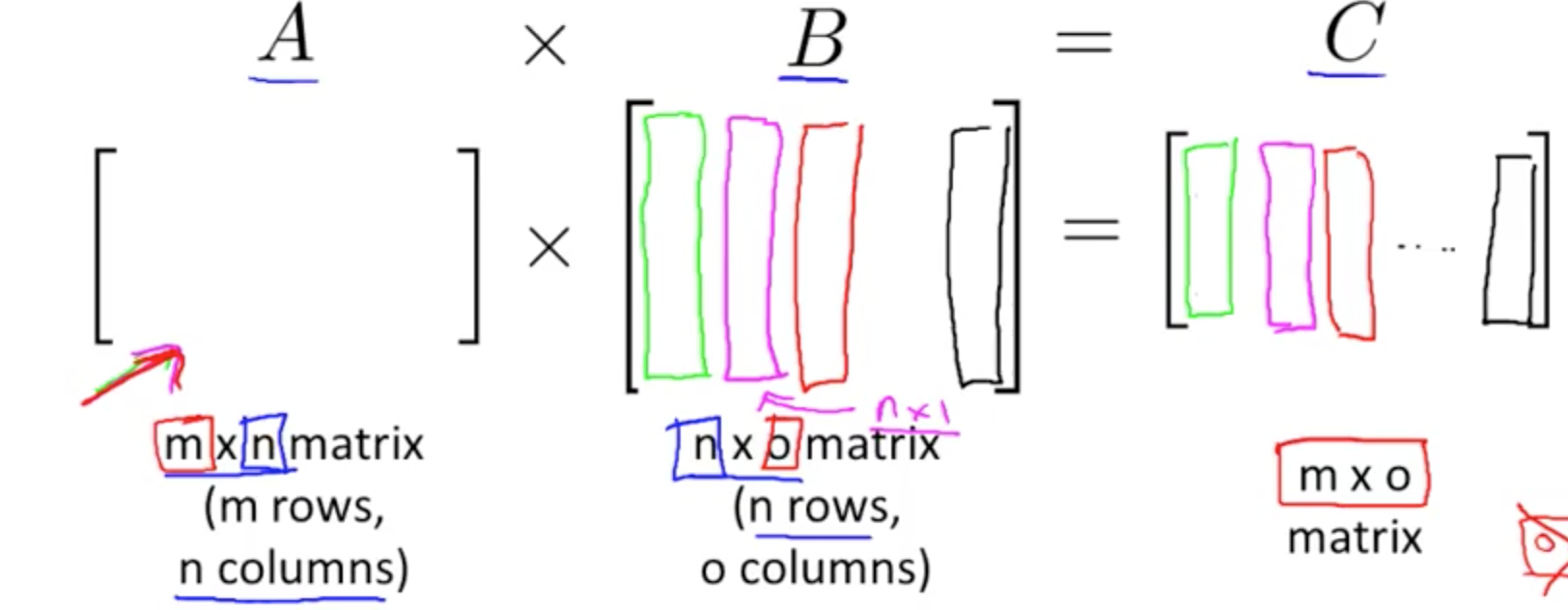
  • prediction = data_matrix x parameters alt text

4. Matrix Matrix Multiplication

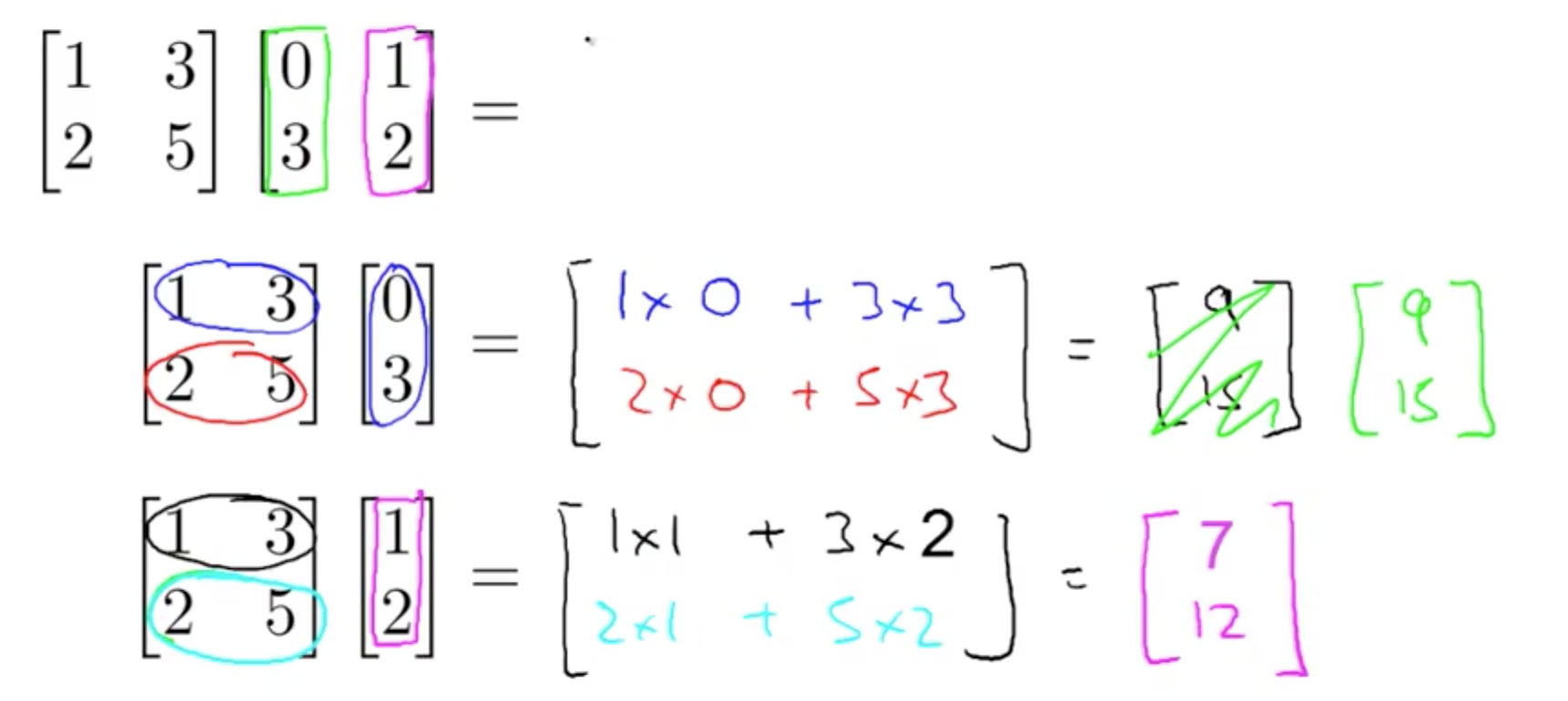
  • Example alt text alt text
  • Theory alt text
  • Application to hypothesis by converting given data to matrix
    • There are linear algebra libraries to do these calculations alt text

5. Properties of Matrix Multiplication

  • Not commutative alt text
  • Associative
    • A x B x C = (A x B) x C = A x (B x C)
  • Identity Matrix alt text

6. Inverse and Transpose

6a. Inverse

  • A * A_inverse = Identity Matrix
  • A_inverse = pinv(A)
    • You can use octave code pinv(A)
  • Matrices without inverse –> singular or degenerate alt text

6b. Transpose

  • Example and theory alt text
Tags: machine_learning