Evaluating machine learning algorithms, training set, cross validation set, test set, bias, variance, learning curves and improving algorithm performance.
1. Evaluating Learning Algorithm
I would like to give full credits to the respective authors as these are my personal python notebooks taken from deep learning courses from Andrew Ng, Data School and Udemy :) This is a simple python notebook hosted generously through Github Pages that is on my main personal notes repository on https://github.com/ritchieng/ritchieng.github.io. They are meant for my personal review but I have open-source my repository of personal notes as a lot of people found it useful.
1a. Deciding what to try next
- Suppose you have implemented regularized linear regression to predict housing prices
- However, when you test your hypothesis your hypothesis on new set of houses, you find that it makes unacceptably large errors
- You can do the following
- Get more training data
- Smaller set of features
- Get additional features
- Try adding polynomial features
- Try decreasing lambda
- Try increasing lambda
- Typically people randomly choose these avenues and then figure out it may not be suitable
- There is a simple technique to weed out avenues that are not suitable
- Machine Learning Diagnostic
- Test that you can run to gain insight what is or isn’t working with a learning algorithm and gain guidance as to how best to improve its performance
- Diagnostics can take time to implement, but doing so can be a very good use of your time
- But it’s worth the time compared to spending months on unsuitable avenues
- Machine Learning Diagnostic
- You can do the following
- However, when you test your hypothesis your hypothesis on new set of houses, you find that it makes unacceptably large errors
1b. Evaluating a hypothesis
- In fitting parameters to your training data, you would want to lower your training error to the minimum
- How to tell if over-fitting?
- You can plot for few features
- For many features: training/testing procedure
- Split into 2 portions
- Training set
- Test set
- Randomly re-order data before splitting
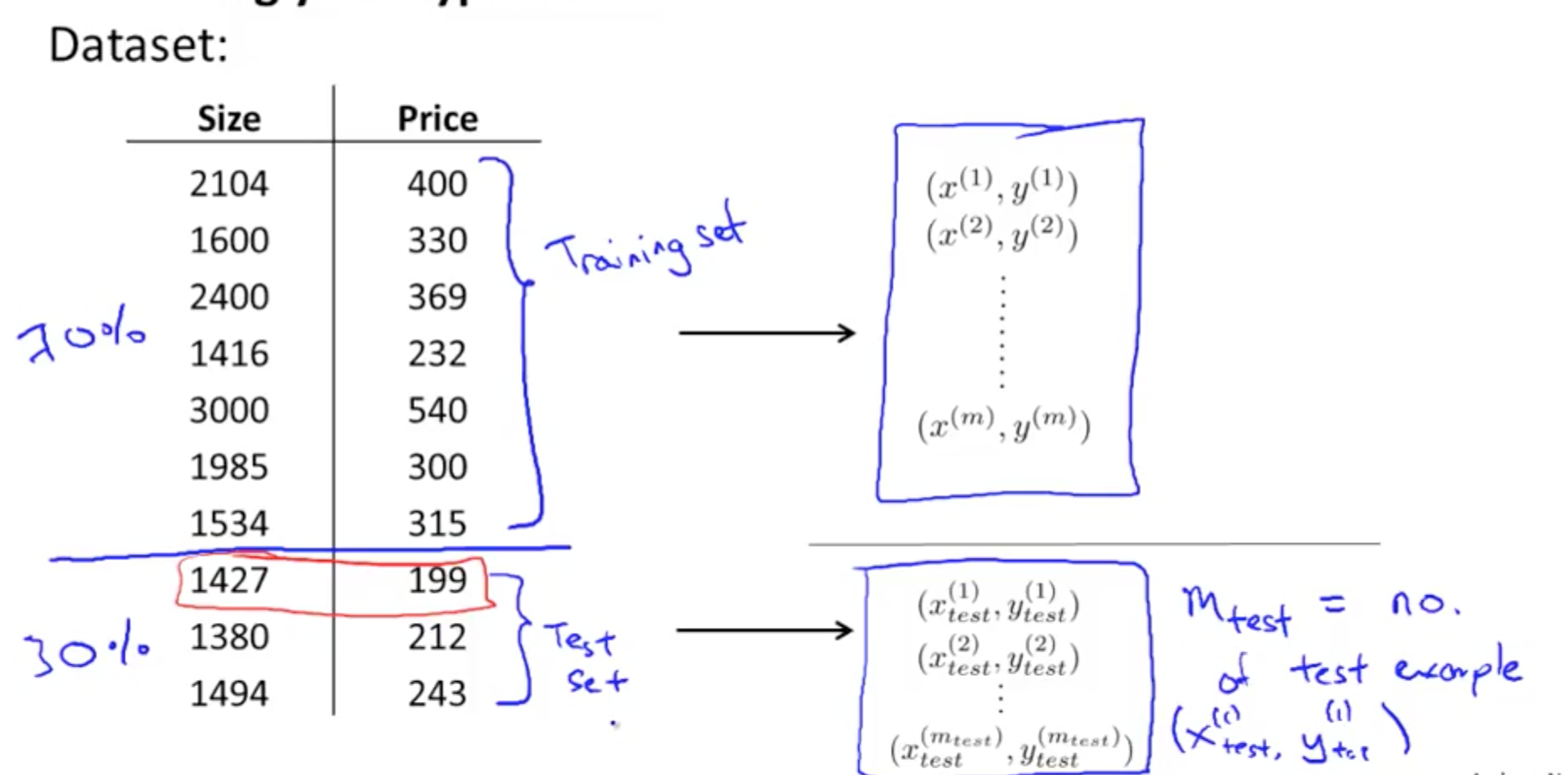
- Randomly re-order data before splitting
- Split into 2 portions
- Training/testing procedure: linear regression

- Training/testing procedure: logistic regression

1c. Model selection and Train/Validation/Test Sets
- Model selection
- We can create an extra parameter d which is the degree of polynomial
- You can measure the test error on each parameter θ
- If you choose d = 5 and to determine how well the model generalizes, you can report test set error on Jtest(θ5)
- But there is a problem: Jtest(θ5) is likely an optimistic estimate of generalization error

- But there is a problem: Jtest(θ5) is likely an optimistic estimate of generalization error
- If you choose d = 5 and to determine how well the model generalizes, you can report test set error on Jtest(θ5)
- To address the problem, we can do the following
- Split data into 3 categories
- Training set
- Cross validation set or Validation set or CV
- Test set

- You would have the following 3 errors
- Training error
- Cross validation (CV) error
- Test error

- Split data into 3 categories
- We would test on cross-validation sets
- Pick hypothesis with lowest CV error

- Pick hypothesis with lowest CV error
2. Bias vs Variance
2a. Diagnosing vs Variance
- When you run an algorithm and it doesn’t do as well as you hope, it typically has a high bias or high variance issue
- High bias (underfitting)
- High variance (overfitting)
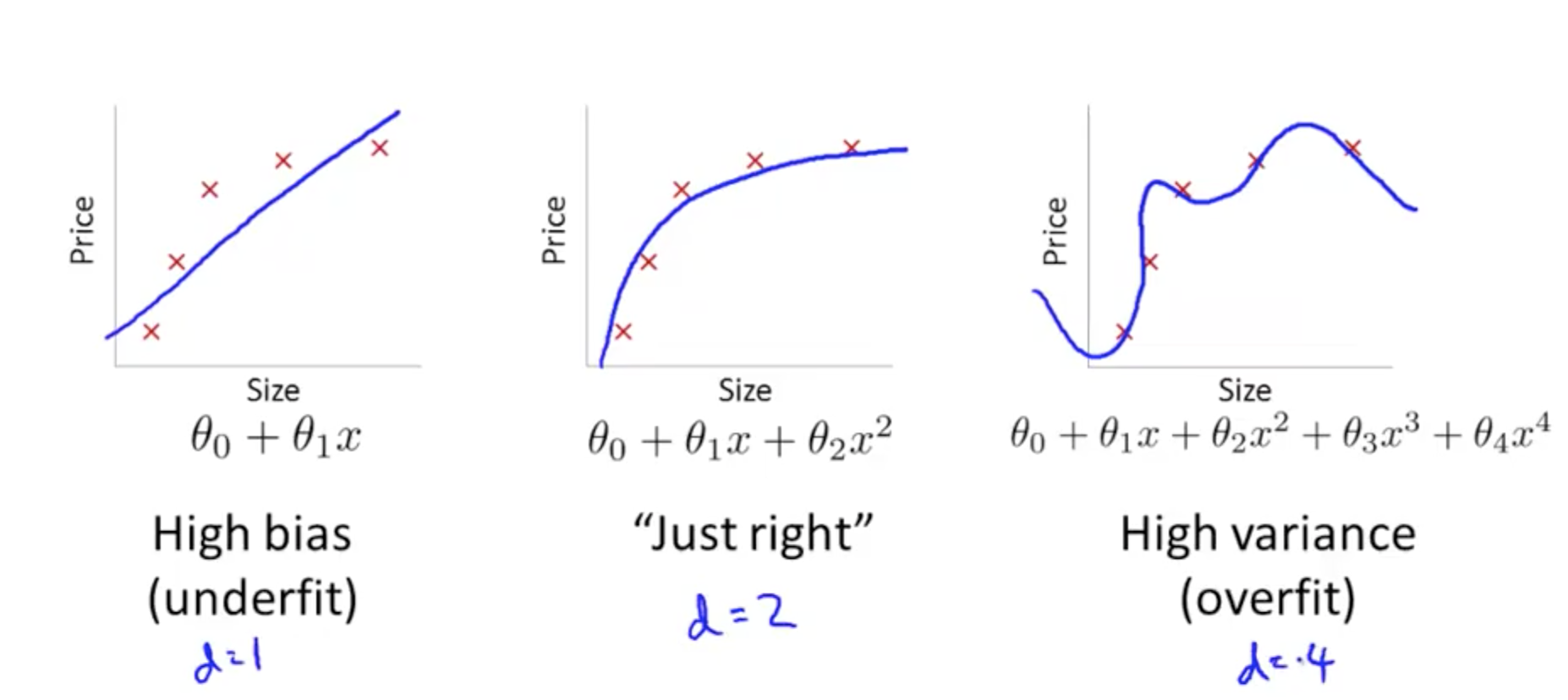
- Plot error against degree of polynomial, d
- As you increase your polynomial, d,
- Training error decreases from underfitting to overfitting
- Cross validation (CV) error example
- d = 1: underfitting, high CV error
- d = 2: lower CV error due to better fit
- d = 4: overfitting, high CV error
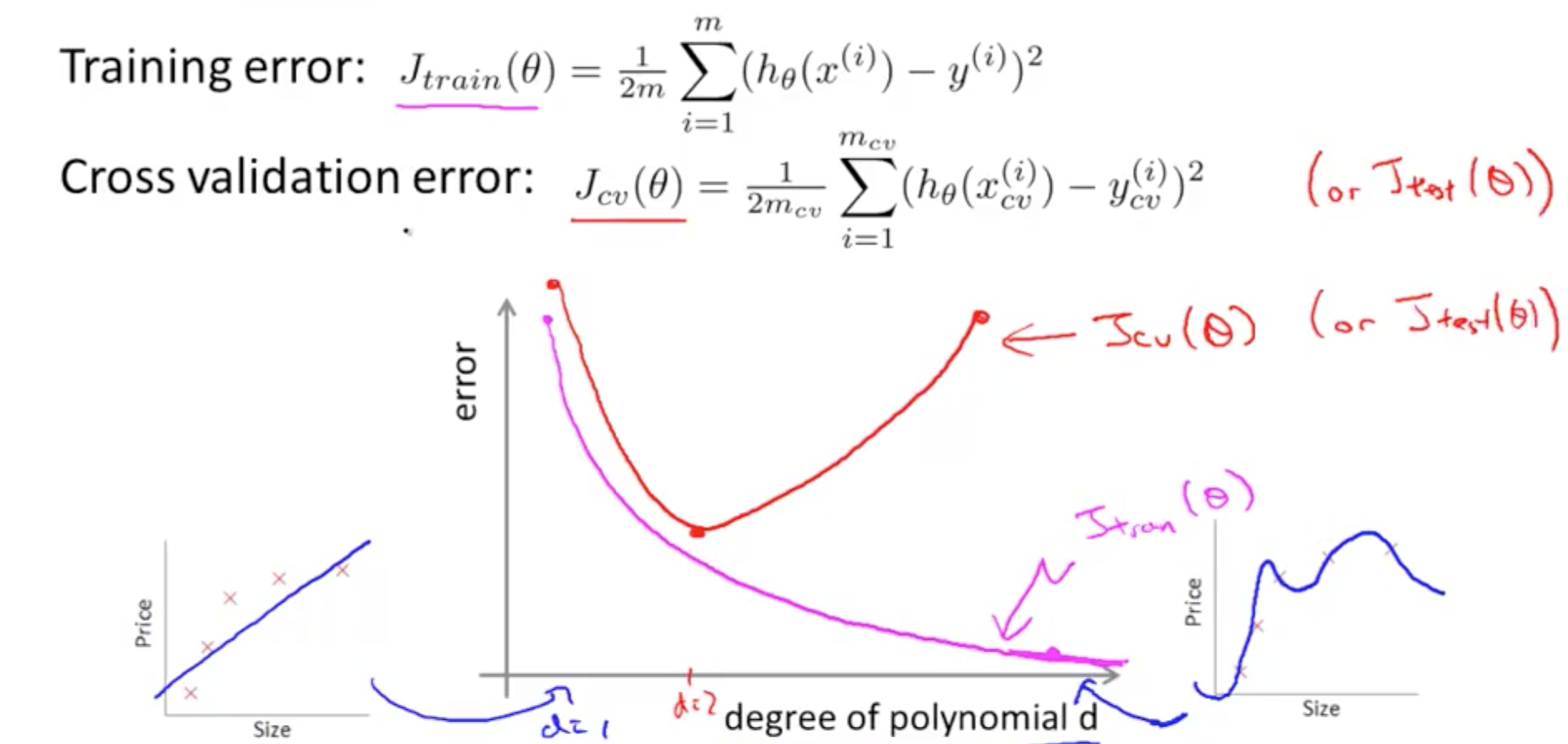
- As you increase your polynomial, d,
- How do we distinguish between a high bias or a high variance issue?
- High Bias Error
- High Jtrain(θ)
- Jtrain(θ) = Jcv(θ)
- High Variance Error
- Low Jtrain(θ)
- Jcv(θ) » Jtrain(θ)
- Much greater as seen on the right of the graph

- Much greater as seen on the right of the graph
- High Bias Error
2b. Regularization and Bias/Variance
- Linear regression with regularization
- Large λ
- High bias (underfit)
- Small λ
- High variance (overfit)
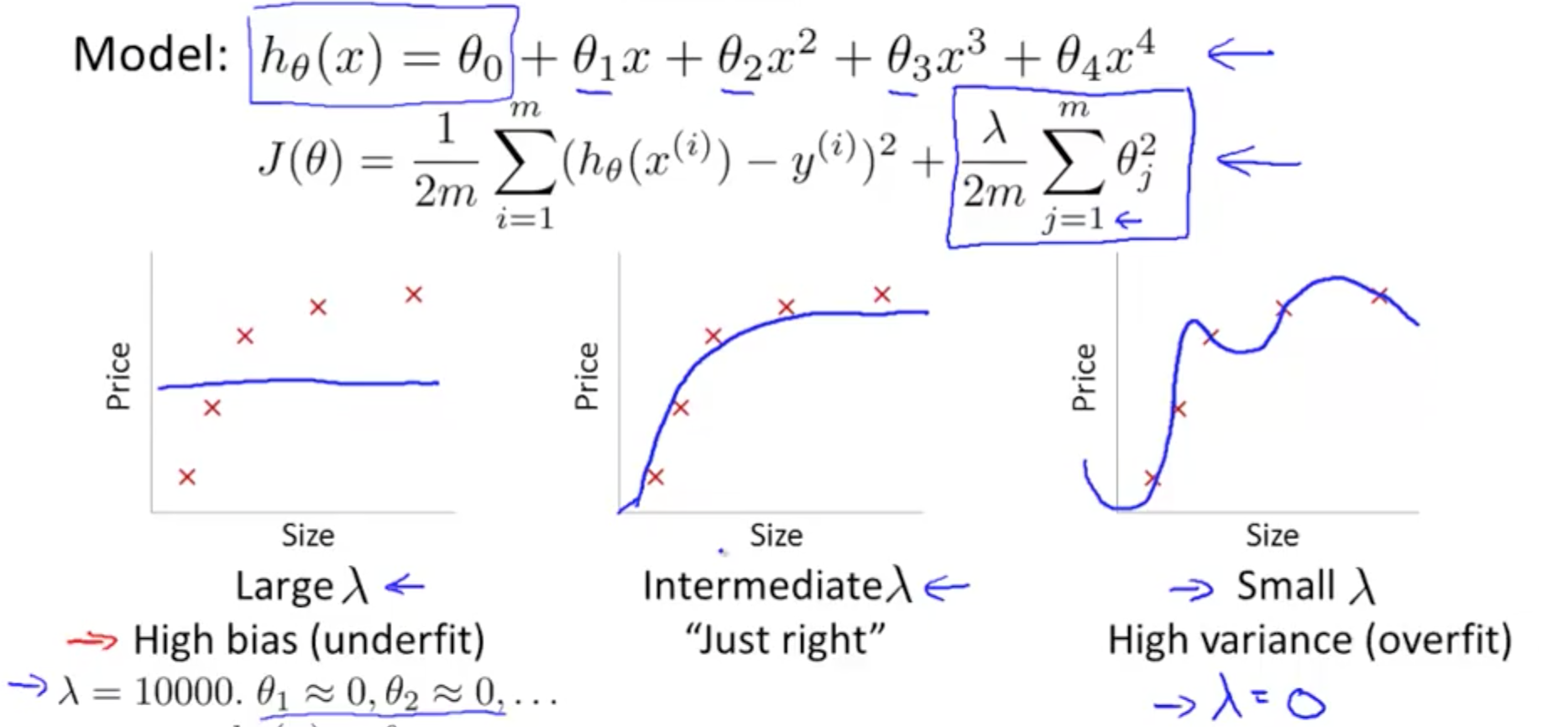
- High variance (overfit)
- Large λ
- So how do we choose a good value of λ?
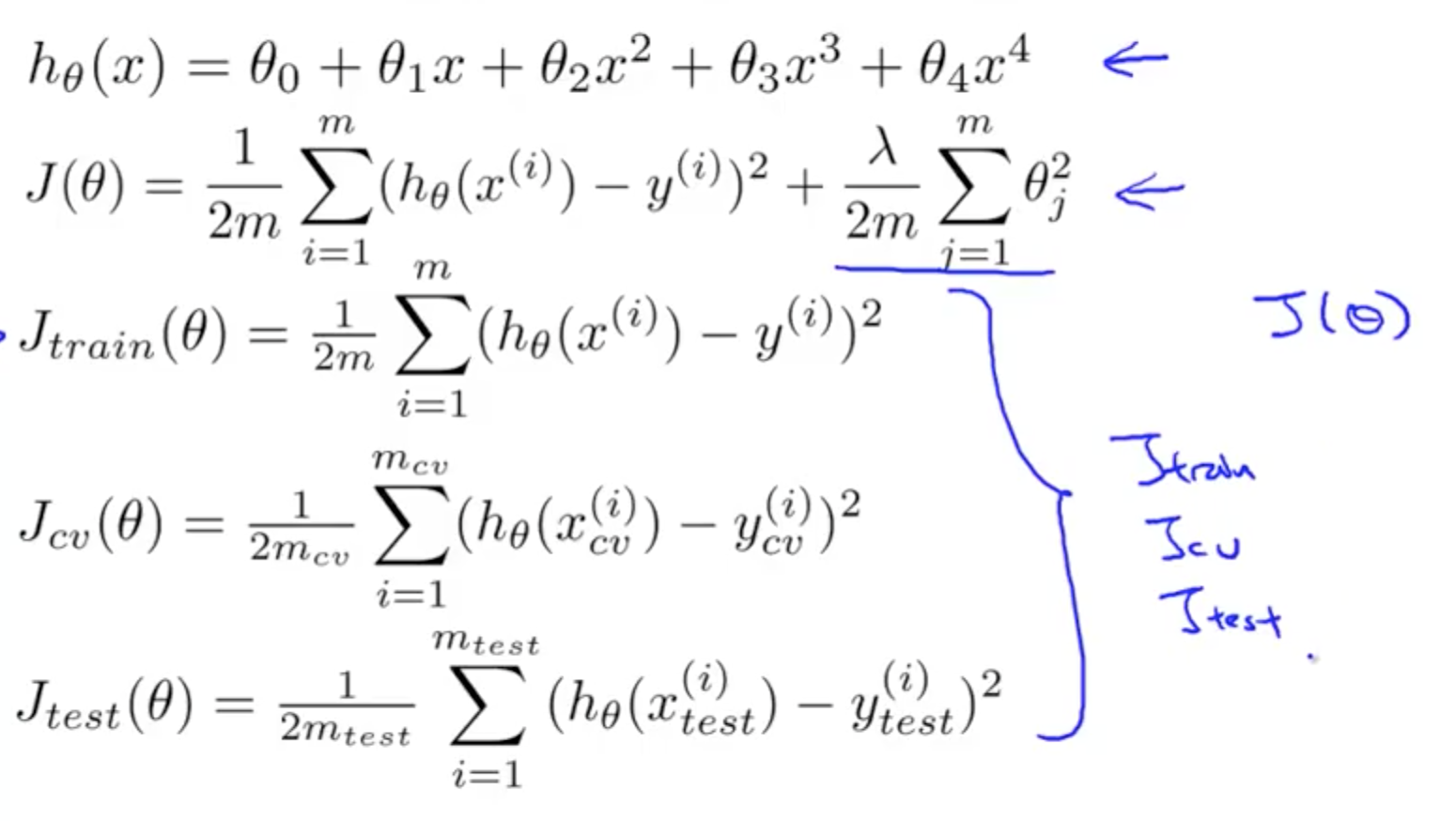
- H(θ): algorithm; hypothesis
- J(θ): cost function; optimization objective
- Jtrain(θ), Jcv(θ), Jtest(θ): optimization objectives without regularization terms
- Steps
- Try λ in multiples of 2 on J(θ)
- Minimise J(θ) to get θ
- Try λ in multiples of 2 on Jcv(θ)
- Minimise Jcv(θ) to get θ
- Choose lowest Jcv(θ), θ_low
- Where θ_low is θ_5 in the example since Jcv(θ_5) is the lowest
- Pick Jcv(θ), θ_low
- Try for Jtest(θ_low)

- Try for Jtest(θ_low)
- Try λ in multiples of 2 on J(θ)
- How CV and test error vary as we vary λ?
- Jtrain(θ)
- Small λ
- Regularization term is small
- Hypothesis fits better to the data
- Low Jtrain(θ)
- Large λ
- Regularization term is large
- Hypothesis does not fit well to the data
- High Jtrain(θ)
- Small λ
- Jcv(θ)
- Large λ
- Regularization term is large
- High bias (underfitting)
- Large Jcv(θ)
- Small λ
- Regularization term is small
- High variance (overfitting)
- Small Jcv(θ)
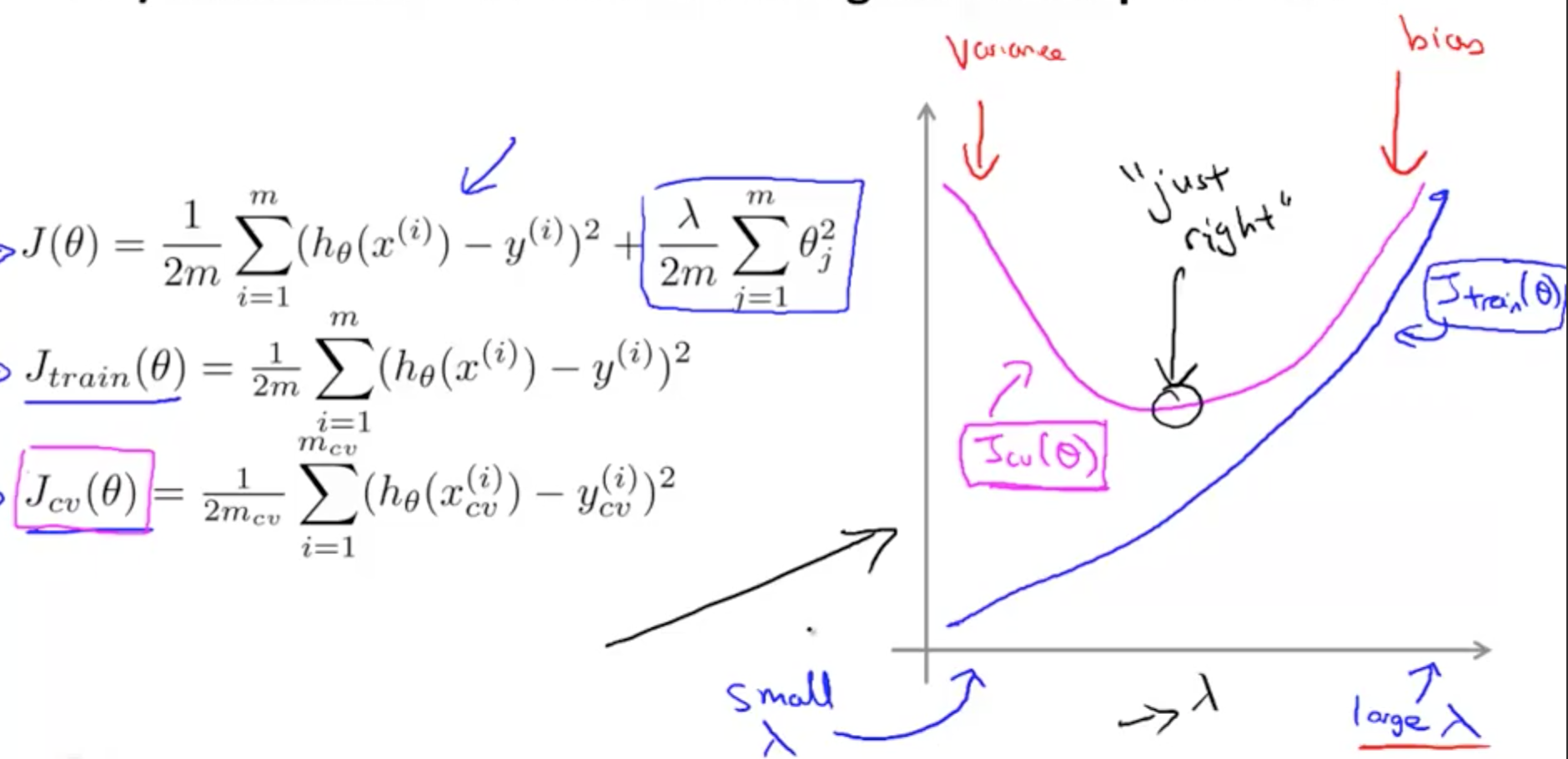
- Large λ
- For a real dataset, the graph is messier, but the general trend is similar
- Jtrain(θ)
2c. Learning Curves
- What is the effect of m, number of training examples, on training error?
- For m = 1, 2, 3 in the example
- If the training set is small
- Easier to fit every single training example perfectly
- Your training error = 0 or small
- For m = 4, 5, 6
- If the training set grows larger
- Harder to fit every single training example perfectly
- Your training error increases
- In general, when m increases, training error increases
- For m = 1, 2, 3 in the example
- What is the effect of m, number of training examples, on cross validation error?
- The more data you have, where m increases
- Your cross validation error decreases
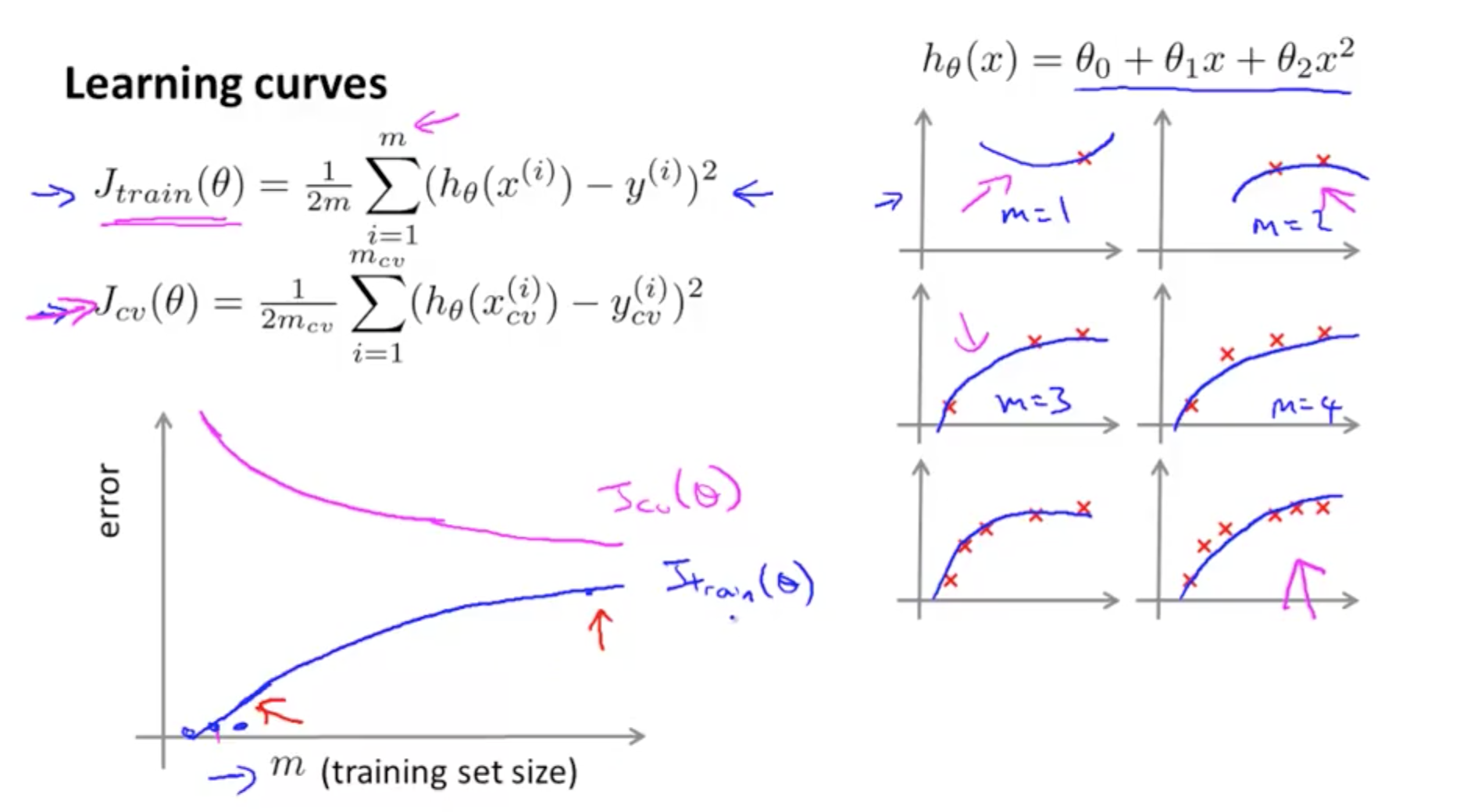
- Your cross validation error decreases
- The more data you have, where m increases
- High Bias (Underfit)
- Poor performance on both training and test sets
- Your cross validation error decreases, but it decreases to a high value
- Even if you have large m, you still have a straight line with a high bias
- Your cross validation error would still be high
- Your training error increases close to the level achieve from your cross validation error
- If a learning algorithm is suffering from high bias, getting more training data will not (by itself) help much
- As seen from the two graphs, even with a higher m, there’s no use collecting more data to decrease your cross validation error
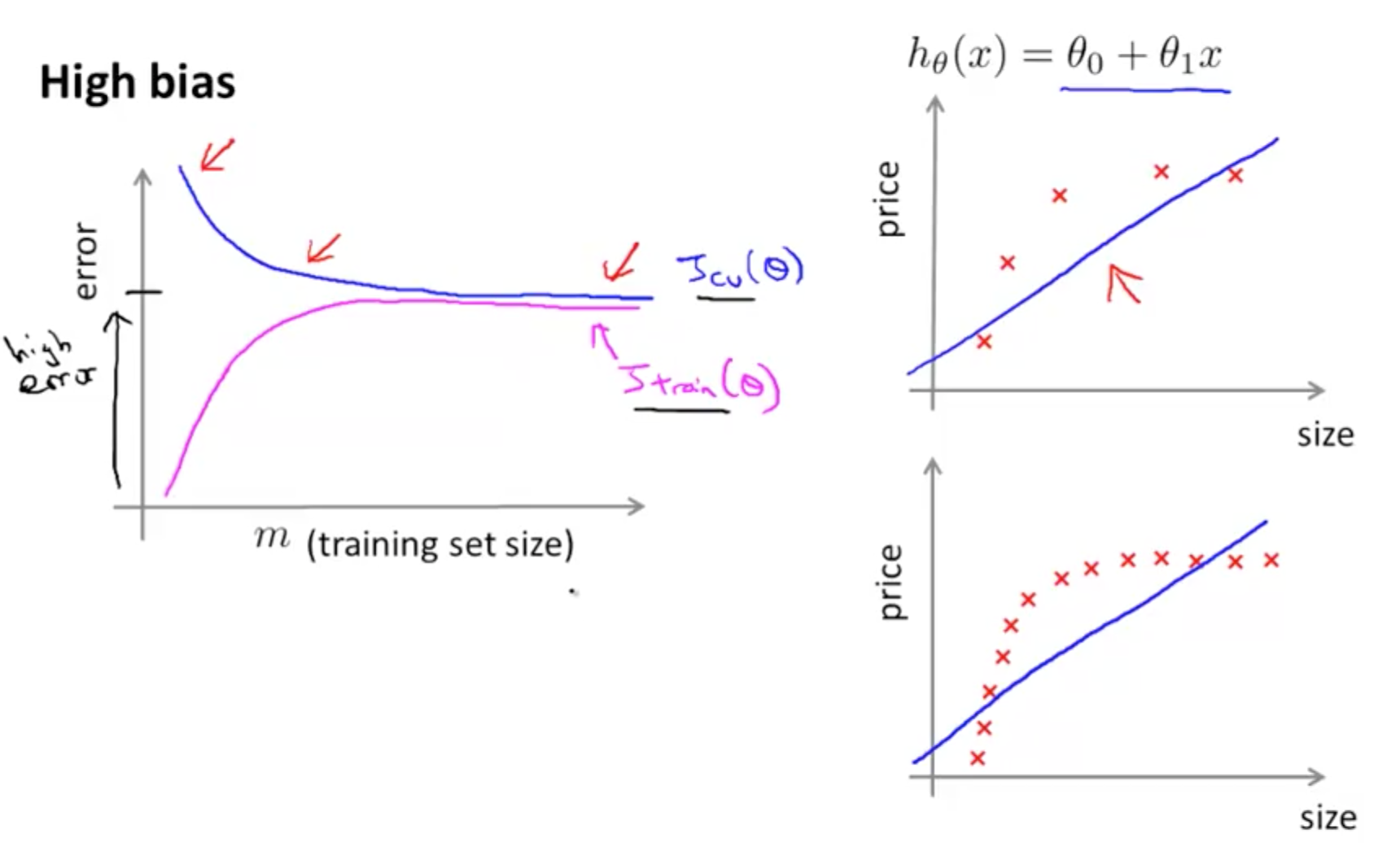
- As seen from the two graphs, even with a higher m, there’s no use collecting more data to decrease your cross validation error
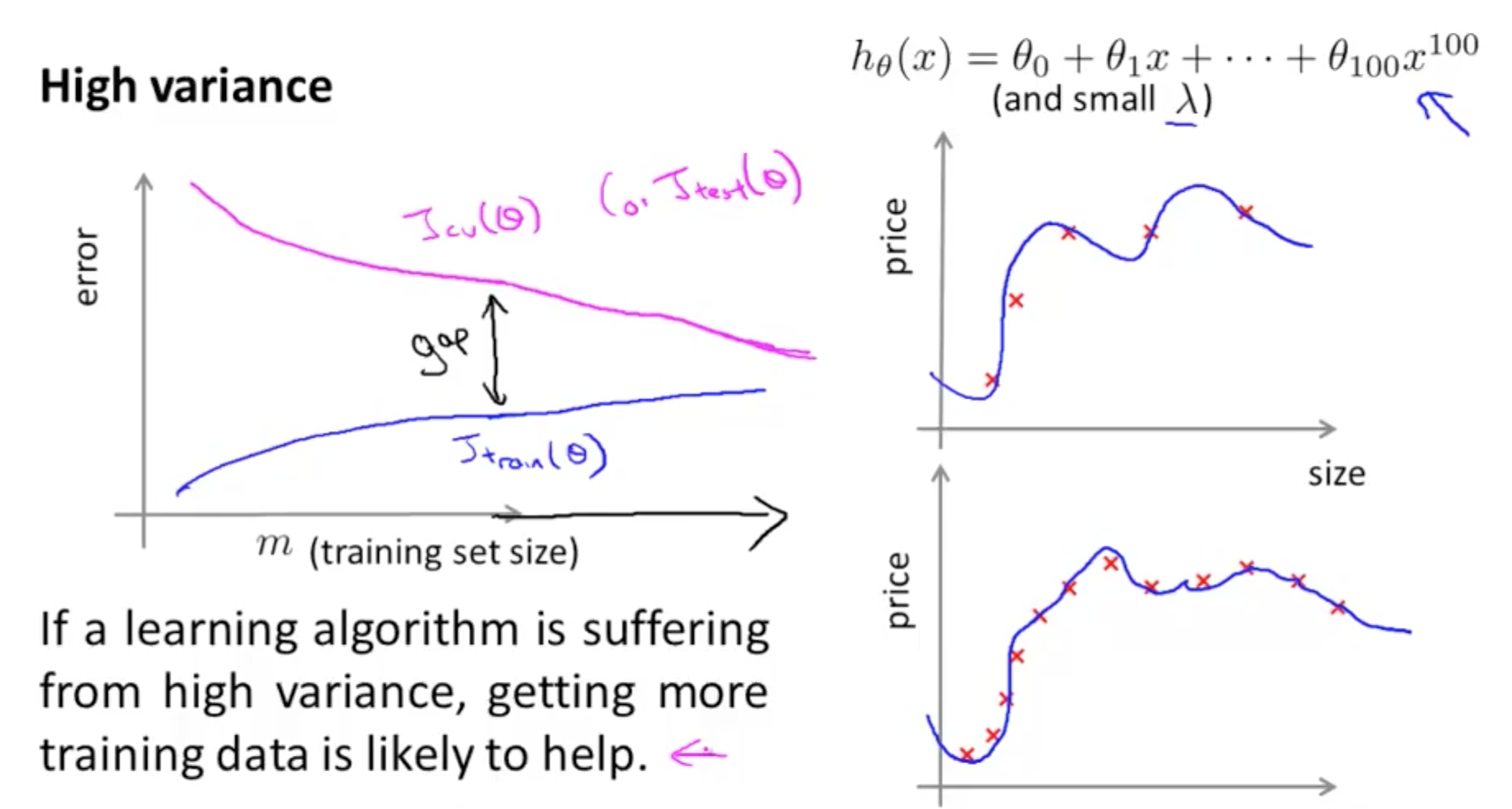
- High Variance (Overfit)
- Gap in errors where training error is low but test error is high
- Training error would remain small
- This happens when you use a small λ
- Your training error increases with m because it becomes harder to fit your data
- Cross validation error would remain high
- This happens when you use a small λ
- If a learning algorithm is suffering from high variance, getting more data is likely to help
2d. Improving Algorithm Performance
- Suppose you have implemented regularized linear regression to predict housing prices
- However, when you test your hypothesis your hypothesis on new set of houses, you find that it makes unacceptably large errors
- You can do the following
- Get more training data
- Fixes high variance
- Smaller set of features
- Fixes high variance
- Features are too complicated
- Fixes high variance
- Get additional features
- Fixes high bias
- Features are too simple
- Fixes high bias
- Try adding polynomial features
- Fixes high bias
- Too low d
- Fixes high bias
- Try decreasing lambda
- Fixes high bias
- Because you would have a smaller regularized term, giving more importance to other features
- Fixes high bias
- Try increasing lambda
- Fixes high variance
- Because you would have a larger regularized term, giving less importance to other features
- Fixes high variance
- Get more training data
- You can do the following
- However, when you test your hypothesis your hypothesis on new set of houses, you find that it makes unacceptably large errors
- Neural Networks and Overfitting
- If you are fitting a neural network, you can use a small or large neural network
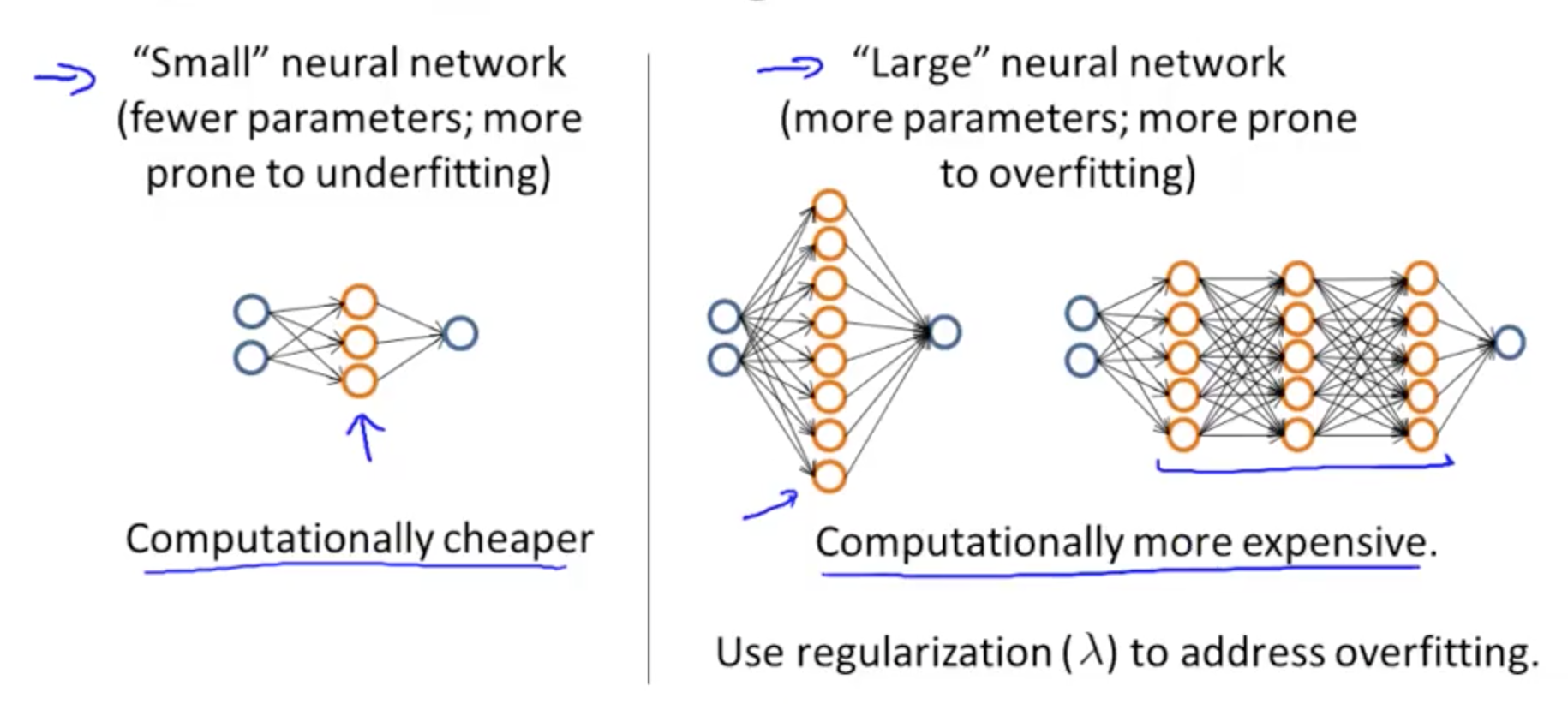
- Small neural network
- 1 hidden layer
- 1 input layer
- 1 output layer
- Computationally cheaper
- Large neural network
- Multiple hidden layers
- 1 input layer
- 1 output layer
- Computationally expensive
- Small neural network
- If you are fitting a neural network, you can use a small or large neural network